Title
题目
Mitigating medical dataset bias by learning adaptive agreement from a biased council
通过从有偏委员会中学习自适应一致性来缓解医疗数据集偏差
01
文献速递介绍
尽管当前人工智能在医学图像分析的诸多领域已达到专家级水平(Topol,2019),但深度学习模型的可信度仍因倾向于学习数据集偏差引发的虚假关联而受到挑战,这导致模型不准确、不可靠且有失公允,阻碍了其在实际临床应用中的普及。尽管这一问题至关重要,但在医学图像分类领域,针对数据集偏差的研究仍较为匮乏。 数据集偏差,或称为“捷径”,通常指与目标模式存在虚假关联的特征。以往研究表明,深度学习模型更倾向于学习这类特征,因为它们更容易被习得(Luo 等,2022b;Nam 等,2020;Shah 等,2020)。具体而言,随机梯度下降(SGD)的训练过程往往会找到简单的解决方案,这被一些人称为“简单性偏差”,且被认为是深度神经网络泛化能力较强的原因之一(Kalimeris 等,2019;Hermann 和 Lampinen,2020;Teney 等,2022)。然而,这种偏好也可能阻碍模型学习更复杂的模式,为模型利用“捷径”快速拟合整个训练数据提供了前提(Shah 等,2020;Geirhos 等,2020;Nam 等,2020)。当非因果因素与目标模式存在虚假关联时,简单性偏差的危害尤为明显。例如,卷积神经网络可能基于胸腔引流管的模式来识别气胸患者(Oakden-Rayner 等,2020;Rueckel 等,2020),而胸腔引流管是一种常见的用于排出胸膜腔内空气或液体的治疗手段。与气胸复杂且模糊的体征相比,胸腔引流管在 X 光片上的模式更清晰,也更容易被识别。类似的研究发现还包括:模型更倾向于学习数据源而非胸部疾病(如图 1 所示)(Luo 等,2022b)、学习性别特征而非气胸(Larrazabal 等,2020),甚至学习侧位标记而非 COVID-19 病变(DeGrave 等,2021)。尽管这类现象被频繁报道,但在医学图像领域,针对数据集偏差的基准测试和解决方案仍然较少。 重新收集数据可以消除数据集偏差,这在概念上简单,但在实际操作中并不可行(Rouzrokh 等,2022)。因此,许多研究尝试通过增加少数群体样本(例如,没有胸腔引流管的气胸病例)的权重来学习稳健的模型(Li 和 Vasconcelos,2019;Sagawa 等,2020)。另一个广泛的研究方向是提出跨不同环境或不同亚组偏移的不变表示学习(Arjovsky 等,2019;Zhang 等,2021;Zhou 等,2022;Tartaglione 等,2021;Zhu 等,2021;Shui 等,2022b,a,2023)。这些方法用算法解决方案替代了对数据收集的需求,但其需要明确的数据集偏差标签,而数据集偏差往往需要在对训练好的模型进行仔细评估和解释后才能被发现(Bluemke 等,2020;DeGrave 等,2021),且明确标记数据集偏差既繁琐又依赖专业知识,因此这些方法的实用性仍较低。 最近的研究探索了在没有明确数据集偏差标签的情况下缓解捷径学习的方法(Sohoni 等,2020;Nam 等,2020;Liu 等,2021;Lee 等,2021;Kim 等,2021;Luo 等,2022b),这些方法大致可分为两阶段方法和单阶段方法。两阶段方法首先捕捉并预测偏差信息,然后基于预测的偏差信息开发群体稳健的学习模型(Sohoni 等,2020;Liu 等,2021;Kim 等,2021;Luo 等,2022b)。然而,这些方法对有偏模型的收敛性较为敏感,并且在群体稳健学习过程中可能引入噪声。相比之下,单阶段方法通常通过将去偏差模型的损失与同时训练的有偏模型的损失进行比较来开发去偏差模型(Nam 等,2020;Lee 等,2021)。通常,这类方法通过增加与有偏模型“偏见”相悖的样本的权重/关注度来实现去偏差。尽管如此,这些方法主要基于启发式的损失加权函数,这可能导致权重过高,并阻碍模型学习目标模式。 以二分类为例,设两个二元变量(y)和(b)分别表示目标特征和偏差特征。为简单起见,如果一个样本的特征与数据集中的虚假关联一致,即(y = b),我们称该样本为偏差一致样本;如果一个样本的特征与虚假关联相反,即(y \neq b),则称该样本为偏差冲突样本。有偏模型可能主要从偏差一致样本中学习,并根据(b)做出决策。当被限制只能从偏差冲突数据中学习时,去偏差模型需要从(y=1)、(b=0)或(y=0)、(b=1)的样本中学习。由于学习区分偏差(b)比学习特征(y)更容易,模型仍然会根据(b)做出决策。因此,启发式地增加偏差冲突样本的权重可能是有害的,一个好的去偏差模型应该从两种类型的样本中学习。 为此,本文提出了“来自有偏委员会的自适应一致性”(Ada-ABC)算法,这是一种单阶段算法,通过平衡从有偏模型的指导中学习一致性和不一致性来实现去偏差。具体而言,使用广义交叉熵损失训练有偏模型,这有助于通过鼓励模型学习更容易的样本来捕捉捷径。为了增强偏差学习能力,我们引入了“偏差委员会”——一个从多样化训练子集中学习到的分类器集合。为了学习去偏差模型,我们提出了一种自适应一致性目标,要求模型与有偏模型的正确决策保持一致,与有偏模型的错误决策产生分歧,而非使用启发式的损失加权函数。本质上,当有偏模型对一个样本分类正确时,即有偏模型做出了正确决策,该样本更有可能是偏差一致样本。因此,学习一致性可以防止去偏差模型在很大程度上忽略具有虚假关联的样本中包含的丰富信息,而学习不一致性进一步促使模型通过没有虚假关联的样本来学习不同的最小值。因此,Ada-ABC 通过同时训练偏差委员会和去偏差模型来实现。此外,我们提供了理论分析,以证明自适应一致性损失迫使去偏差模型学习与有偏模型所捕捉的特征不同的特征。 为了证明我们提出的 Ada-ABC 在缓解医学图像中数据集偏差方面的有效性,我们在四个医学图像数据集的七种不同场景下进行了大量实验,这些数据集存在各种数据集偏差。我们的主要动机是通过一个有组织的基准来探索医学图像偏差这一重要课题,并为这一挑战提出一种最先进的解决方案。我们的主要贡献如下: - 提出了 Ada-ABC,这是一种新颖的单阶段、不依赖偏差标签的框架,用于缓解医学图像分类中的数据集偏差。 - 从理论上证明,利用我们提出的算法,当有偏模型捕捉到偏差信息时,去偏差模型能够学习到目标特征。 - 据我们所知,我们提供了第一个医学去偏差基准,该基准专注于解决来自四个数据集的虚假关联,涵盖七种不同场景,包含各种医学数据集偏差。 - 基于该基准,验证了我们提出的 Ada-ABC 在各种情况下缓解医学数据集偏差的有效性。
Abatract
摘要
Dataset bias in images is an important yet less explored topic in medical images. Deep learning could be prone to learning spurious correlation raised by dataset bias, resulting in inaccurate, unreliable, and unfair models, which impedes its adoption in real-world clinical applications. Despite its significance, there is a dearth of research in the medical image classification domain to address dataset bias. Furthermore, the bias labels are often agnostic, as identifying biases can be laborious and depend on post-hoc interpretation. This paper proposes learning Adaptive Agreement from a Biased Council (Ada-ABC), a debiasing framework that does not rely on explicit bias labels to tackle dataset bias in medical images. Ada-ABC develops a biased council consisting of multiple classifiers optimized with generalized cross entropy loss to learn the dataset bias. A debiasing model is then simultaneously trained under the guidance of the biased council. Specifically, the debiasing model is required to learn adaptive agreement with the biased council by agreeing on the correctly predicted samples and disagreeing on the wrongly predicted samples by the biased council. In this way, the debiasing model could learn the target attribute on the samples without spurious correlations while also avoiding ignoring the rich information in samples with spurious correlations. We theoretically demonstrated that the debiasing model could learn the target features when the biased model successfully captures dataset bias. Moreover, we constructed the first medical debiasing benchmark focusing on addressing spurious correlation from four datasets containing seven different bias scenarios. Our extensive experiments practically showed that our proposed Ada-ABC outperformed competitive approaches, verifying its effectiveness in mitigating dataset bias for medical image classification.
图像中的数据集偏差是医学图像领域一个重要但研究较少的课题。深度学习容易学习到由数据集偏差引发的虚假关联,导致模型不准确、不可靠且有失公允,这阻碍了其在实际临床应用中的普及。尽管这一问题意义重大,但在医学图像分类领域,针对数据集偏差的研究仍较为匮乏。此外,偏差标签往往难以获取,因为识别偏差既费力又依赖事后解释。 本文提出了一种从有偏委员会中学习自适应一致性的去偏差框架(Ada-ABC),该框架无需依赖明确的偏差标签,即可解决医学图像中的数据集偏差问题。Ada-ABC构建了一个由多个分类器组成的有偏委员会,这些分类器通过广义交叉熵损失进行优化,以学习数据集偏差。随后,在有偏委员会的指导下,同步训练一个去偏差模型。具体而言,去偏差模型需要学习与有偏委员会的自适应一致性:对于有偏委员会预测正确的样本,两者保持一致;对于有偏委员会预测错误的样本,两者则产生分歧。通过这种方式,去偏差模型能够在无虚假关联的样本上学习目标属性,同时又不会忽略含虚假关联样本中的丰富信息。 我们从理论上证明,当有偏模型成功捕捉到数据集偏差时,去偏差模型能够学习到目标特征。此外,我们构建了首个医学去偏差基准,该基准聚焦于解决来自4个数据集的虚假关联,涵盖7种不同的偏差场景。大量实验表明,我们提出的Ada-ABC性能优于同类方法,证实了其在缓解医学图像分类中数据集偏差方面的有效性。
Method
方法
3.1. Problem setup Generally, a sample data ?? could contain different attributes, e.g., whether a chest X-ray contains pneumothorax, whether the patient is male, whether a chest drain is applied, etc. Let (??, ??) be the pair of (possibly latent) target and bias attributes, the values of ?? and ?? are binary, where 0 and 1 represent whether the attribute is absent or present, respectively. Specifically, ?? is used for labeling the dataset, and ?? may not be recorded due to limited labeling budget or privacy reasons. We can obtain a dataset = {(??1 , ??1 ), (??2 , ??2 ),…}, where ???? represents the label of ???? . As the data is labeled according to the target attribute, we have ???? = ?? ?? . The dataset is biased as the bias attribute is spuriously correlated to the target attribute, i.e., ???? = ???? for most of the samples. Therefore, ?? can be almost as predictive as ??. We define a bias-aligned sample if ???? = ???? and a bias-conflicting sample if ???? ≠ ???? . Following previous works (Nam et al., 2020; Lee et al., 2021; Luo et al., 2022b), our discussion and experiments focus on the situations where the dataset bias is known to exist while not explicitly labeled. Our main goal is to develop debiasing models that use the target attribute instead of the bias attribute for making decisions. To this end, we propose a one-stage debiasing algorithm, Adaptive Agreement from Biased Council (Ada-ABC), to learn a debiased model without explicit labeling of the bias attributes. As depicted in Fig. 2, Ada-ABC trains two networks simultaneously. A model ???? will be trained with empirical risk minimization (ERM) to learn the shortcuts as much as possible, where ?? represents the mapping function of the model and ?? represents the model’s parameters. The other model ????̃ (the Robust model in Fig. 2) will be trained at the same time via learning adaptive agreement from ???? .
3.1. 问题设定 通常,一个样本数据(x)可能包含不同的属性,例如,胸部X光片是否包含气胸、患者是否为男性、是否使用了胸引流管等。设((y, b))为(可能潜在的)目标属性和偏差属性对,(y)和(b)的值均为二元的,其中0和1分别表示该属性不存在或存在。具体而言,(y)用于标记数据集,而由于标注预算有限或隐私原因,(b)可能未被记录。我们可以得到一个数据集(\mathcal{D} = {(x_1, y_1), (x_2, y_2), \ldots}),其中(y_i)表示(x_i)的标签。由于数据是根据目标属性进行标记的,因此有(y_i = y(x_i))。该数据集存在偏差,因为偏差属性与目标属性存在虚假关联,即对于大多数样本,(b_i = y_i)。因此,(b)的预测能力几乎与(y)相当。我们将(b_i = y_i)的样本定义为偏差一致样本,将(b_i \neq y_i)的样本定义为偏差冲突样本。 遵循先前的研究(Nam等,2020;Lee等,2021;Luo等,2022b),我们的讨论和实验聚焦于数据集偏差已知存在但未被明确标记的情况。我们的主要目标是开发去偏差模型,使其基于目标属性而非偏差属性做出决策。 为此,我们提出了一种单阶段去偏差算法——来自有偏委员会的自适应一致性(Ada-ABC),用于在不明确标记偏差属性的情况下学习去偏差模型。如图2所示,Ada-ABC同时训练两个网络。一个模型(f\theta)将通过经验风险最小化(ERM)进行训练,以尽可能多地学习捷径,其中(f)表示模型的映射函数,(\theta)表示模型的参数。另一个模型(\tilde{f}\phi)(图2中的稳健模型)将通过从(f_\theta)学习自适应一致性来同时进行训练。
Conclusion
结论
Dataset bias in image processing is an essential topic (Torralba and Efros, 2011; Liu and He, 2025; Rajpurkar et al., 2024) yet less explored in medical images. Combating dataset bias relies on both building less biased datasets and developing more capable models (Liu and He, 2025). In this paper, we investigated different types of dataset biases in medical images with an organized medical debiasing benchmark (MBD), including data source, sex, treatments, and age, which could all lead to shortcut learning and performance drops. To note, the performance drop of a deep-learning model stems from multiple aspects, such as label noises, image noises, overfitting, insufficient training, etc. Hence, detecting dataset bias remains tedious work, where one would still need to first observe whether the model is biased and further detect the type of bias. Consequently, our collected datasets were based on previously reported dataset biases for clinically important binary classification tasks, such as pneumonia classification, pneumothorax classification, and ischemic heart disease risk assessment. In addition, our current work does not aim to solve the problem from the very start of finding the dataset biases, but relies on the knowledge of the existence of dataset bias. Still, the proposed Ada-ABC could effectively learn target features from biased data without extensive bias labeling in one-stage joint training of two models, which largely alleviates the labor for extensive bias labeling. We believe that MBD and AdaABC would serve as groundwork for more exploration and solutions to medical image dataset biases. In summary, this paper proposes a simple yet effective one-stage debiasing framework, Adaptive Agreement from Biased Council (AdaABC). Ada-ABC is based on simultaneous training of a biased network and a multi-head debiasing network. The biased model is developed to capture the bias information in the dataset, using a bias council trained with the generalized cross entropy loss to amplify the learning preference for the samples with spurious correlation. Then, the debiasing model adaptively learns to agree or disagree with the biased model on the samples with or without spurious correlation, respectively, under the supervision of our proposed adaptive learning loss. We provided theoretical analysis to prove that the debiasing model could learn the targeted feature when the biased model successfully captures the biasinformation. Further, we constructed the first medical debiasing benchmark to our best knowledge, which consists of four datasets with seven different bias scenarios. Based on MBD, we validated the effectiveness of Ada-ABC in mitigating dataset bias with extensive experiments and showed that it achieved state-of-the-art performance on the benchmark. We demonstrated that, both theoretically and practically, Ada-ABC provides a promising way for more accurate, fair, and trustworthy medical image analysis.
图像处理中的数据集偏差是一个重要课题(Torralba 和 Efros,2011;Liu 和 He,2025;Rajpurkar 等,2024),但在医学图像领域的研究仍较为匮乏。对抗数据集偏差既需要构建偏差较小的数据集,也需要开发更具能力的模型(Liu 和 He,2025)。 在本文中,我们通过一个有组织的医学去偏差基准(MBD),研究了医学图像中不同类型的数据集偏差,包括数据来源、性别、治疗方式和年龄等,这些都可能导致捷径学习和性能下降。需要注意的是,深度学习模型的性能下降源于多个方面,如标签噪声、图像噪声、过拟合、训练不足等。因此,检测数据集偏差仍然是一项繁琐的工作,研究者需要首先观察模型是否存在偏差,进而检测偏差的类型。 基于此,我们收集的数据集是基于先前报道的、针对具有临床重要性的二分类任务的数据集偏差,例如肺炎分类、气胸分类和缺血性心脏病风险评估。此外,我们当前的工作并非旨在从发现数据集偏差的初始阶段就解决问题,而是依赖于已知数据集偏差存在这一前提。尽管如此,所提出的Ada-ABC能够在无需大量偏差标注的情况下,通过两个模型的单阶段联合训练,有效地从有偏数据中学习目标特征,这在很大程度上减轻了大量偏差标注的工作量。我们相信,医学去偏差基准(MBD)和Ada-ABC将为医学图像数据集偏差的进一步探索和解决方案奠定基础。 总之,本文提出了一种简单而有效的单阶段去偏差框架——来自有偏委员会的自适应一致性(Ada-ABC)。Ada-ABC基于同时训练一个有偏网络和一个多头去偏差网络。有偏模型旨在捕捉数据集中的偏差信息,它利用通过广义交叉熵损失训练的偏差委员会,来强化对具有虚假关联样本的学习偏好。然后,在我们提出的自适应学习损失的监督下,去偏差模型针对具有虚假关联和不具有虚假关联的样本,分别自适应地学习与有偏模型保持一致或产生分歧。我们通过理论分析证明,当有偏模型成功捕捉到偏差信息时,去偏差模型能够学习到目标特征。 此外,据我们所知,我们构建了第一个医学去偏差基准,该基准包含四个数据集,涵盖七种不同的偏差场景。基于该基准,我们通过大量实验验证了Ada-ABC在缓解数据集偏差方面的有效性,并表明它在该基准上取得了最先进的性能。我们从理论和实践两方面证明,Ada-ABC为更准确、公平和可信的医学图像分析提供了一种有前景的方法。
Figure
图

Fig. 1. Dataset bias in medical image classification could lead to inaccurate and untrustworthy results. Here, the source of data and whether the patient contains pneumonia are spuriously correlated. A biased model would make decisions based on the data source while ignoring the patterns of the lesions. Our goal is to learn a robust model that can make bias-invariant decisions from the biased training set.
图1. 医学图像分类中的数据集偏差可能导致不准确且不可靠的结果。在此,数据来源与患者是否患有肺炎存在虚假关联。有偏模型会基于数据来源做出决策,而忽略病变模式。我们的目标是从有偏训练集中学习一个稳健的模型,使其能够做出不受偏差影响的决策。

Fig. 2. The Framework of Ada-ABC. The goal is to develop a debiasing model which is robust to dataset biases (e.g., caused by spurious correlation between the data source and health condition). A bias council, consisting of multiple classification heads (i.e., ℎ1, ℎ2, …), is trained with empirical risk minimization (ERM) and generates prediction ??. The second model (i.e., the Robust model) is jointly trained and required to agree with the correct predictions made by the ERM model and disagree with the wrong predictions, using the objective ?????? + (1 − ??)?????? . Under such an adaptive agreement learning scheme, a different decision-making rule can be learned from the samples w/o spurious correlations, while rich information from the samples w/ spurious correlation can be preserved as well.
图2. Ada-ABC框架。其目标是开发一个对数据集偏差具有稳健性的去偏差模型(例如,由数据来源与健康状况之间的虚假关联所导致的偏差)。一个由多个分类头(即ℎ1、ℎ2、……)组成的偏差委员会,通过经验风险最小化(ERM)进行训练,并生成预测结果(p_b)。第二个模型(即图中的稳健模型)被联合训练,要求其与ERM模型的正确预测保持一致,与错误预测产生分歧,所使用的目标函数为(\lambda\mathcal{L}{agree} + (1-\lambda)\mathcal{L}{disagree})。在这种自适应一致性学习方案下,能够从无虚假关联的样本中学习到不同的决策规则,同时也能保留有虚假关联样本中的丰富信息。

Fig. 3. Effects of the hyper-parameters ?? and number of heads. The first row shows the results on SbP dataset with ?? = 99%: (a) The changes of aligned AUC and conflicting AUC w.r.t. the change of ?? (# heads = 16). (b) The changes of overall AUC and balanced AUC w.r.t. the change of ?? (# heads = 16). © The changes of overall AUC and balanced AUC w.r.t. the change of number of heads (?? = 100). The second row shows the results on OL3I dataset: (d) The changes of aligned AUC and conflicting AUC w.r.t. the change of ?? (# heads = 8). (e) The changes of overall AUC and balanced AUC w.r.t. the change of ?? (# heads = 8). (f) The changes of overall AUC and balanced AUC w.r.t. the change of number of heads (?? = 300).
图3. 超参数(\lambda)和分类头数量的影响。第一行展示了在SbP数据集(偏差占比(b=99\%))上的结果:(a) 随着(\lambda)的变化,偏差一致样本的AUC和偏差冲突样本的AUC的变化(分类头数量=16)。(b) 随着(\lambda)的变化,整体AUC和平衡AUC的变化(分类头数量=16)。© 随着分类头数量的变化,整体AUC和平衡AUC的变化((\lambda=100))。第二行展示了在OL3I数据集上的结果:(d) 随着(\lambda)的变化,偏差一致样本的AUC和偏差冲突样本的AUC的变化(分类头数量=8)。(e) 随着(\lambda)的变化,整体AUC和平衡AUC的变化(分类头数量=8)。(f) 随着分类头数量的变化,整体AUC和平衡AUC的变化((\lambda=300))。

Fig. 4. The decision boundaries by (a) an ERM model that learns a simple solution; another model that learns to (b) purely agree with the ERM model, or © purely disagree with the ERM model, (d) or adaptively agree or disagree with the ERM model. Details are best appreciated when enlarged.
图4. 不同模型的决策边界:(a) 一个学习简单解决方案的经验风险最小化(ERM)模型;(b) 一个完全与ERM模型保持一致的模型;© 一个完全与ERM模型相悖的模型;(d) 一个能自适应地与ERM模型保持一致或产生分歧的模型。放大后可更清晰地查看细节。

Fig. 5. The saliency maps by the ERM model (2nd row) and the debiasing model by Ada-ABC (3rd row). Samples from columns 1–4 are from SbP, SeXbP, DbP, and OL3I, respectively, and contains pneumonia, pneumothorax, pneumothorax, and a one-year risk of ischemic heart disease, respectively. Both models made correct predictions but were looking for different reasons.
图5. 经验风险最小化(ERM)模型(第二行)和Ada-ABC去偏差模型(第三行)的显著性图。第1-4列的样本分别来自SbP、SeXbP、DbP和OL3I数据集,分别对应肺炎、气胸、气胸和一年缺血性心脏病风险的相关样本。两个模型都做出了正确的预测,但所依据的原因不同。
Table
表
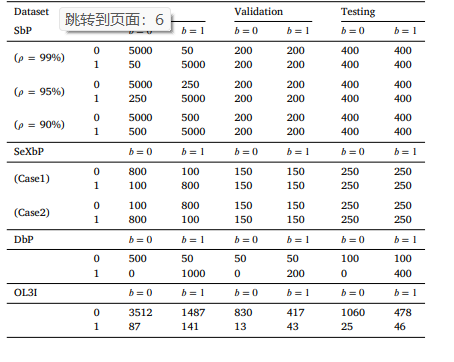
Table 1 Detailed number of data in different datasets. ?? and ?? represent the target and bias attribute, respectively. The meaning of ?? and ?? for each dataset can be found in Section 4.1.
表1 不同数据集的详细数据量。(y)和(b)分别代表目标属性和偏差属性。每个数据集的(y)和(b)的具体含义可参见4.1节。

Table 2 Comparison on the debiasing benchmark using AUC. For methods do not use bias labels, the best and second-best performance (on the balanced AUC and overall AUC) are in red and blue, respectively. The last row is the average of the mean overall AUC from all seven scenarios. ??: the ratio of bias-aligned samples in the training set.
表2 基于AUC的去偏差基准测试比较。对于不使用偏差标签的方法,其在平衡AUC和整体AUC上的最佳性能和次佳性能分别用红色和蓝色标注。最后一行为所有七个场景的平均整体AUC的均值。(\gamma):训练集中偏差一致样本的比例。

Table 3 Comparison on the debiasing benchmark using accuracy (ACC). For methods do not use bias labels, the best and second-best performance (on the balanced ACC and overall ACC) are in red and blue, respectively. The last row is the average of the mean overall ACC from all seven scenarios. ??: the ratio of bias-aligned samples in the training set. Note that sometimes the balanced ACC and overall ACC have the same value as they are mathematically the same on a testing set with equal number of subgroups.
表3 基于准确率(ACC)的去偏差基准测试比较。对于不使用偏差标签的方法,其在平衡准确率(balanced ACC)和整体准确率(overall ACC)上的最佳性能和次佳性能分别用红色和蓝色标注。最后一行为所有七个场景的平均整体准确率的均值。(\gamma):训练集中偏差一致样本的比例。注意,有时平衡准确率和整体准确率数值相同,这是因为在子组数量相等的测试集上,二者在数学上是一致的。

Table 4 Summary of final hyper-parameters for each dataset.
表4 每个数据集的最终超参数汇总。
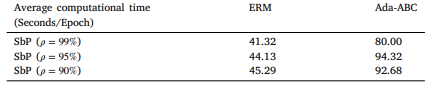
Table 5 Average computational time used of different methods on each dataset.
表5 不同方法在各数据集上的平均计算时间。

Table 6 Comparison on SbP with moderate bias. For methods do not use bias labels, the best and second-best performance (on the balanced AUC and overall AUC) are in red and blue, respectively. The last row is the average of the mean overall AUC from all seven scenarios. ??: the ratio of bias-aligned samples in the training set. SbP (?? = 75%): ?? = 3, # head = 1; SbP (?? = 50%): ?? = 0.1, # head = 32
表6 中等偏差下SbP数据集的比较结果。对于不使用偏差标签的方法,其在平衡AUC和整体AUC上的最佳性能和次佳性能分别用红色和蓝色标注。最后一行为所有七个场景的平均整体AUC的均值。(\gamma):训练集中偏差一致样本的比例。SbP((\gamma=75\%)):(\lambda=3),分类头数量=1;SbP((\gamma=50\%)):(\lambda=0.1),分类头数量=32。

Table 7 Comparison between ERM and Ada-ABC trained from scratches.
表7 经验风险最小化(ERM)模型与从零开始训练的Ada-ABC模型的比较。