Title

题目

A deep learning approach to multi-fiber parameter estimation and uncertainty quantification in diffusion MRI

一种用于扩散磁共振成像（MRI）中多纤维参数估计和不确定性量化的深度学习方法

01

文献速递介绍

扩散磁共振成像（dMRI）是一种广泛用于在体内研究大脑结构的成像方式（巴塞尔和皮耶波利，1996）。在扩散磁共振成像中，脉冲梯度自旋回波序列用于使成像信号对水分子的局部扩散敏感。由于局部神经组织环境对这种扩散的影响，分析这些信号可以揭示潜在的大脑组织微观结构的特性，从而提供对人类活体大脑细胞组织结构的洞察。这些微观结构特性可作为可解释的生物标志物，并被应用于各种神经科学任务中，例如疾病诊断、神经外科手术规划和精准医学（埃赛德等人，2017；杰莱斯库和布德，2017；诺维科夫等人，2019；皮耶里等人，2021）。然而，从观测到的扩散磁共振成像信号中推断这些微观结构特征的稳健统计和计算方法的发展，因该问题常常具有不适定性而变得复杂（基谢列夫，2017）。应对这些挑战需要设计出不仅能提高估计准确性，而且能够进行严格的不确定性量化以评估估计结果可靠性的方法。 微观结构推断需要两个要素：一个是将组织参数与观测信号联系起来的模型，另一个是从观测数据中恢复这些参数的估计过程。关于前者，扩散磁共振成像中的一个标准生物物理模型是卷积模型： (f(\boldsymbol{p}, b) \approx \mathcal{G}g|b, \boldsymbol{\xi} := \int{\mathbb{S}²} h{\mathcal{G}} (\boldsymbol{p}^\top \boldsymbol{u}|b, \boldsymbol{\xi}) g(\boldsymbol{u}) d\boldsymbol{u})  （1） （简和韦穆里，2007），其中观测到的扩散信号(f(\boldsymbol{p}, b))是两个由实验控制的采集参数的函数：(b)矢量(\boldsymbol{p} \in \mathbb{S}²)，它是所施加的磁场梯度的方向；以及(b)值(b \in \mathbb{R}^+0)，它是一个与梯度强度和扩散时间相关的复合参数。正演映射(\mathcal{G})是一个具有核函数(h{\mathcal{G}})的旋转不变积分算子，由(b)值和局部组织参数(\boldsymbol{\xi})参数化，(g)是(\mathbb{S}²)上的一个密度函数，被称为（纤维）“方向分布函数”（ODF）。方向分布函数描述了体素中相干排列的白质纤维群体的方向轮廓，而核函数(h{\mathcal{G}})的形式则指定了潜在的扩散生物物理模型。公式（1）中的近似关系是为了突出在推导生物物理模型时所使用的各种简化假设，例如潜在组织几何结构的理想化模型、高斯相位假设、轴突内和轴突外组织区域之间可忽略的水交换等等。 已经提出了多种在模型（1）下进行参数估计的方法。当方向推断是主要目标时，一类流行的去卷积方法采用两阶段方法：首先固定正演模型，例如使用全局估计值(\hat{\boldsymbol{\xi}})，然后通过采用各种促进平滑性和/或稀疏性的先验，在(g)的函数空间中解决由此产生的线性逆问题（德斯科特奥等人，2007，2009；图尔尼耶等人，2007；德劳里耶 - 高蒂尔和马尔齐利亚诺，2013；尤里森等人，2014；米哈伊洛维奇等人，2011；拉蒂等人，2013；塞德拉尔等人，2021；埃拉尔迪等人，2021，2024；孔萨格拉等人，2024）。另一方面，一类专注于微观结构的方法以(\boldsymbol{\xi})为目标，同时将方向信息视为干扰因素，利用模型（1）所暗示的(f)和(\boldsymbol{\xi})之间的旋转不变性，推导出将信号的旋转不变量与核参数联系起来的非线性回归，并使用直接优化（诺维科夫等人，2018）或基于学习的方法（赖泽特等人，2017；刁和杰莱斯库，2023；贾莱和帕洛姆博，2024）进行参数估计。专注于同时估计方向和核参数的方法在一定程度上受到限制。典型的方法是通过使用标准数值优化器来解决（通常是非凸的）逆问题，以近似最大似然点估计（MLE）（张等人，2012；帕纳焦塔基等人，2012；杰莱斯库等人，2016；哈姆斯等人，2017）。或者，在贝叶斯框架下，可以应用基于通用马尔可夫链蒙特卡罗（MCMC）的采样方案进行推断（贾布迪等人，2007；亚历山大，2008；鲍威尔等人，2021），或者通过基于字典的方法进行两阶段凸重构，并采用诱导稀疏性的正则化（达杜奇等人，2015；叶，2017）。 由于成像分辨率有限，一个体素通常包含多个不同的纤维群体，每个纤维群体都可能表现出独特的微观结构特征（德桑蒂斯等人，2016；宁等人，2019）。模型（1）的一个显著局限性是生物物理参数(\boldsymbol{\xi})被限制在一个体素内的所有纤维之间共享。为了进行纤维特异性推断，对（1）的一个自然扩展是混合卷积模型： (f(\boldsymbol{p}, b) \approx \sum{i = 1}^{n} \int{\mathbb{S}²} w_i h{\mathcal{G}} (\boldsymbol{p}^\top \boldsymbol{u}|b, \boldsymbol{\xi}i) g(\boldsymbol{u}|\boldsymbol{m}i) d\boldsymbol{u})，(\sum{i = 1}^{n} w_i = 1)  （2） 其中(\boldsymbol{\xi}i)是第(i)根纤维的核参数，(\boldsymbol{m}_i \in \mathbb{S}²)是第(i)个方向（方向分布函数模式），(w_i \geq 0)是混合权重，(n)是穿过成像体素的纤维数量，实际上所有这些都是未知的，必须进行估计。将模型（1）中用于联合方向和核参数估计的标准方法应用于混合公式（2）并非易事。参数空间维度的增加加剧了与估计问题的非凸性相关的问题，这可能导致潜在的大量局部解，从而降低了用于寻找最大似然估计的标准优化程序的有效性。已经提出了对基于字典的方法的多纤维扩展（奥里亚等人，2015）；然而，构建字典所需的对潜在参数空间的离散采样可能会带来重大的计算挑战，特别是在处理复杂的生物物理核函数或纳入理想的诱导稀疏性的正则化时（亚普等人，2016）。此外，标准优化方法和基于字典的方法都没有明确地解决其估计中的不确定性量化问题。在贝叶斯公式中也出现了问题，因为非线性正演映射可能导致复杂的多模态后验分布，这给基于有效马尔可夫链蒙特卡罗的采样带来了计算挑战（姚等人，2022）。此外，由于需要选择(n)，又出现了一个新的挑战。标准的模型选择方法，例如赤池信息准则/贝叶斯信息准则（AIC/BIC）（塔贝洛等人，2012；王等人，2016），需要为所有的(n)形成最大似然估计，这会导致不必要的重复模型拟合。对未知的(n)进行完全的贝叶斯积分需要扩展采样方案，以允许变化的维度参数空间（卡登和克鲁格尔，2012），这进一步加剧了计算问题。此外，对于(n > 1)，这种方法必须处理所谓的“标签切换”问题（斯蒂芬斯，2000）。 尽管专门为在（2）下进行全参数推断而开发的方法有限，但我们注意到已经开发了几种基于扩散信号直接基展开的混合模型的相关方法。具体来说，图赫等人（2002）提出了一种混合扩散张量模型，通过多次初始化的梯度下降进行参数估计，拉蒂等人（2009）使用混合沃森模型分解信号，并使用非线性最小二乘法进行参数估计，马尔科姆等人（2010）在纤维束成像的背景下使用无迹卡尔曼滤波器（UKF）推断混合张量模型。塔贝洛等人（2012）和王等人（2016）提出了（不同的）对混合扩散张量模型的替代重新参数化，以提高参数的可识别性，并开发了专门的优化程序，其初始化通过更简单的近似模型的最优值来选择。请注意，除了无迹卡尔曼滤波器方法（该方法利用沿纤维束的先验来规范问题）之外，所有这些方法都促进了某种形式的（不理想的）重复模型拟合，以避免与非凸性相关的问题和/或用于选择(n)。此外，只有无迹卡尔曼滤波器对参数估计中的不确定性进行了量化，然而，这些不确定性量化仅在纤维束成像期间且在纤维数量固定（因此参数空间固定）的情况下形成。 受这些缺点的启发，在这项工作中，我们针对标准扩散磁共振成像数据采集设计下的（2）式形式的模型，提出了一种用于全参数估计和不确定性量化的新方法。为了避免与同时推断所有模型参数相关的上述复杂性，我们的方法采用了一种顺序方法，将问题分解为两个阶段：一个用于方向推断和模型选择的边缘子问题，以及一个用于其余核参数的条件子问题。在第一阶段，一个具有对称性感知的深度神经网络近似从信号(f)直接到方向分布函数(g)的逆映射。这种公式有效地排除了核参数的影响，允许通过(g)的最大值对纤维数量及其方向进行简单的非参数估计。在第二阶段，我们表明，在给定方向的条件下，通过解决一个标准优化问题，模型的重新参数化允许将观测信号有效地“解混”为纤维特定的特征。然后，这些解混后的特征被用作深度条件密度估计器的输入，该估计器推断纤维特定的核参数。深度逆模型通过模拟进行训练，然后应用于观测数据，这分摊了最终推断算法的许多步骤，从而能够开发出在计算上可扩展的（重）采样方法，用于对所有模型参数进行不确定性量化。 本文的其余部分组织如下。第2节概述了所考虑的生物物理正演模型和测量模型，探讨了参数的可识别性，并讨论了合成数据的生成。第3节详细介绍了所提出的参数估计和不确定性量化方法。第4节提供了在合成数据集和体内数据集上的实现细节和实验评估，包括与相关替代方法的比较。第5节对结果进行了进一步讨论，并提出了未来研究的方向。第6节给出了总结性结论。

Aastract

摘要

Diffusion MRI (dMRI) is the primary imaging modality used to study brain microstructure in vivo. Reliable andcomputationally efficient parameter inference for common dMRI biophysical models is a challenging inverseproblem, due to factors such as variable dimensionalities (reflecting the unknown number of distinct whitematter fiber populations in a voxel), low signal-to-noise ratios, and non-linear forward models. These challengeshave led many existing methods to use biologically implausible simplified models to stabilize estimation,for instance, assuming shared microstructure across all fiber populations within a voxel. In this work, we manageable subproblems. These subproblems are solved using deep neural networks tailored to problemspecific structure and symmetry, and trained via simulation. The resulting inference procedure is largelyamortized, enabling scalable parameter estimation and uncertainty quantification across all model parameters.Simulation studies and real imaging data analysis using the Human Connectome Project (HCP) demonstratethe advantages of our method over standard alternatives. In the case of the standard model of diffusion, ourresults show that under HCP-like acquisition schemes, estimates for extra-cellular parallel diffusivity are highlyuncertain, while those for the intra-cellular volume fraction can be estimated with relatively high precision.

扩散磁共振成像（dMRI）是用于在体内研究大脑微观结构的主要成像方式。对于常见的扩散磁共振成像生物物理模型而言，进行可靠且计算高效的参数推断是一个具有挑战性的逆问题，这是由多种因素导致的，例如维度的可变性（反映了体素中不同白质纤维群体数量的未知性）、低信噪比，以及非线性的正演模型。这些挑战使得许多现有的方法采用在生物学上不合理的简化模型来稳定估计结果，比如，假设在一个体素内的所有纤维群体具有相同的微观结构。 在这项工作中，我们将该问题分解为若干个易于处理的子问题。这些子问题通过针对特定问题的结构和对称性量身定制的深度神经网络来解决，并通过模拟进行训练。由此产生的推断过程在很大程度上是可分摊计算的，从而能够对所有模型参数进行可扩展的参数估计和不确定性量化。 使用人类连接组计划（HCP）数据进行的模拟研究和实际成像数据分析表明，我们的方法相较于标准的替代方法具有优势。在标准的扩散模型的情况下，我们的结果显示，在类似于人类连接组计划的采集方案下，细胞外平行扩散率的估计值具有高度的不确定性，而细胞内体积分数的估计值则可以以相对较高的精度得出。

Method

方法

In this section, we present our method for estimation and uncertainty quantification for all model parameters. A high-level schematicoverview of the proposed methodology is presented in Fig. 4. Additional supporting technical details can be found in supplementalSection S3.

在本节中，我们将介绍用于对所有模型参数进行估计和不确定性量化的方法。所提出方法的高层次示意性概述如图4所示。更多辅助性的技术细节可在补充材料的第S3节中找到。

Conclusion

结论

In this work, we propose a novel method for biophysical parameterestimation and uncertainty quantification in general mixture deconvolution models of brain microstructure using diffusion MRI data. Insteadof inferring all model parameters simultaneously, our approach uses aseries of deep neural network-based inverse models, each tailored todifferent marginal and conditional subproblems and trained througsimulations. The inverse modules are then applied sequentially to observed imaging data for full parameter inference. In simulation studies,we show that the proposed method generally outperforms standardcompeting approaches, both in terms of lower errors and computationaltimes, while also providing well-calibrated uncertainties that can becomputed rapidly. Qualitative analysis of our method using in vivodiffusion data from the Human Connectome Project shows promisingresults in accurately capturing fiber specific microstructural properties.

在这项工作中，我们提出了一种新的方法，用于利用扩散磁共振成像（MRI）数据，在大脑微观结构的一般混合去卷积模型中进行生物物理参数估计和不确定性量化。我们的方法并非同时推断所有模型参数，而是使用了一系列基于深度神经网络的逆模型，每个逆模型都针对不同的边缘和条件子问题进行了定制，并通过模拟进行训练。然后，依次将这些逆模块应用于观测到的成像数据，以进行全参数推断。 在模拟研究中，我们表明，所提出的方法在误差更低和计算时间更短这两方面，总体上优于标准的竞争方法，同时还能快速计算出经过良好校准的不确定性。通过使用来自人类连接组计划的体内扩散数据对我们的方法进行定性分析，结果显示，在准确捕捉纤维特异性微观结构特性方面，该方法取得了令人鼓舞的成果。

Figure

图

Fig. 1. The standard model of diffusion in white matter decomposes the per-voxel diffusion signal contributions into a mixture of intra and extra axonal components. Multiple distinctfiber populations can be accommodated under a mixture formulation. The observed signal can be approximated as a mixture of convolutions between the multi-compartmentalkernel function and the corresponding ODF mode

图1. 白质中的标准扩散模型将每个体素的扩散信号贡献分解为轴突内和轴突外成分的混合。在混合公式下可以考虑多个不同的纤维群体。观测到的信号可以近似为多隔室核函数与相应的方向分布函数（ODF）模式之间卷积的混合。

Fig. 2. (A) Multi-shell sampling design. (B) Kernel decay curves for two different parameterizations, with SNR ≈ 16. Note that, while 𝐷**𝑒 ∥ differs significantly between the twocurves (red and green), the measured signals are virtually indistinguishable from each other.

图2：（A）多壳层采样设计。（B）两种不同参数化的核衰减曲线，信噪比约为16。请注意，尽管两条曲线（红色和绿色）之间的细胞外平行扩散率(D_e^{\parallel})差异显著，但测量得到的信号实际上彼此难以区分。

Fig. 3. (Left plot) True signal function (colored surface) and noisy observations at the observed 𝒕 ∗ 𝑙,𝑚’s (black stars). (Right plots) True signal decomposes additively over the 1Dmarginal kernel decay curves.

图3：（左图）真实信号函数（彩色曲面）以及在观测到的(\boldsymbol{t}^*_{l,m})处的含噪观测值（黑色星号）。（右图）真实信号可按一维边缘核衰减曲线进行加法分解。  

Fig. 4. Outline of the methodology. The inversion algorithm is trained in two stages. In the first stage, the orientation inverter is trained to map signals, with varying kernels andmeasurement errors, to the underlying ODF using synthetic data generated via Algorithm S3 (supplemental text). The number and peaks of the ODF estimate the fiber orientations,which are then input, along with the signal, into the demixing procedure by solving the optimization problem in Eq. (16). The signal curves are then used as fiber-specific summarystatistics to train a deep mixture density estimator, which approximates the conditional posterior of the 𝑖’th fiber’s microstructure. This training utilizes synthetic data generatedwith Algorithm S4 (supplemental text). After training, the inversion algorithm can be applied to real brain signals for fast parameter inference and uncertainty quantification viaAlgorithm 1.

图4. 方法概述。反演算法分两个阶段进行训练。在第一阶段，使用通过算法S3（补充文本）生成的合成数据，对方向反演器进行训练，使其能够将具有不同核函数和测量误差的信号映射到潜在的方向分布函数（ODF）上。方向分布函数的数量和峰值可估计出纤维的方向，然后将这些方向与信号一起，通过求解公式（16）中的优化问题，输入到解混过程中。接着，信号曲线被用作特定纤维的汇总统计量，以训练一个深度混合密度估计器，该估计器可近似第(i)根纤维微观结构的条件后验概率。此训练使用通过算法S4（补充文本）生成的合成数据。训练完成后，反演算法可应用于真实的大脑信号，通过算法1实现快速的参数推断和不确定性量化。

Fig. 5. Density-colored scatter plots for the 𝑛 = 1 case showing the relationship between ground truth (x-axis) and estimated parameters (y-axis) for all test-set examples for eachmethod (columns).

图5：(n = 1)情况下的密度着色散点图，展示了每种方法（各列）在所有测试集示例中，真实值（横轴）与估计参数值（纵轴）之间的关系。

Fig. 6. ODF field estimates (top left) and per-voxel average angular dispersion (AD) (top right) over a coronal cross section of the HCP-YA subject. Magnified views of the ODFfield from representative ROIs are provided in the middle panels. The bottom panels show the results of the full parameter inference (posterior distributions) using Algorithm 1for the encircled voxel

图6：人类连接组计划青年成人组（HCP-YA）受试者冠状面横截面的方向分布函数（ODF）场估计值（左上角）和每个体素的平均角度离散度（AD）（右上角）。中间各图提供了来自代表性感兴趣区域（ROI）的ODF场放大视图。底部各图展示了使用算法1对圈出的体素进行全参数推断（后验分布）的结果。

Fig. 7. (Left) Fiber cluster colored by the along tract posterior mean for each kernel parameter. (Right) Histograms of posterior samples at all points along the ‘‘most centraltract’’ in the cluster (as measured by the spatial curve depth)

图7：（左图）根据每个核参数沿纤维束的后验均值进行着色的纤维簇。（右图）纤维簇中沿 “最中心纤维束”（通过空间曲线深度来衡量）上所有点的后验样本的直方图 。

Table

表

Table 1Synthetic data test-set averages for proportion of correct peaks (PCP), average angular errors (AE) and inference time (time) for each method

表1合成数据测试集的相关平均值，包括每种方法的正确峰值比例（PCP）、平均角度误差（AE）以及推断时间（time）

Table 2Average absolute error and bias for kernel parameter estimators for the synthetic testdata. Results averaged over fibers in the multi-fiber cases.

表2 针对合成测试数据的核参数估计器的平均绝对误差和偏差。在多纤维情况中，结果是对所有纤维取平均值得到的。

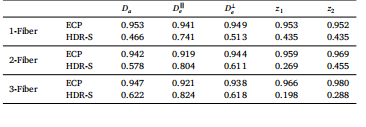
Table 3Empirical Coverage Proportion (ECP) and High Density Regions Size (HDR-S) forbiophysical parameter uncertainty quantification.

表3 用于生物物理参数不确定性量化的经验覆盖比例（ECP）和高密度区域大小（HDR-S）。