Title
题目
Personalized predictions of Glioblastoma infiltration: Mathematical models, Physics-Informed Neural Networks and multimodal scans
胶质母细胞瘤浸润的个性化预测:数学模型、物理信息神经网络和多模态扫描
01
文献速递介绍
胶质母细胞瘤(Glioblastoma, GBM)是一种常见且侵袭性极强的脑肿瘤,其中位生存期为15个月(Stupp等,2014, 2005)。目前的标准治疗包括诊断后立即切除可见肿瘤,随后进行放疗和化疗以针对残留肿瘤(Fernandes等,2017)。尽管治疗强度较高,GBM的预后仍然较差,几乎所有病例均会复发。高复发率的主要原因是其侵袭性特性。GBM不会形成明确的边界,而是侵入周围外观正常的脑组织(Souhami等,2004;Halperin等,1989)。肿瘤细胞的浸润模式具有异质性,在患者之间差异显著。因此,放疗的标准临床靶区(CTV),通常在可见肿瘤外延伸1.5–3厘米,可能无法提供最佳的覆盖和分布(Stupp等,2005)。背景与挑战 为了改进放疗计划设计,关键步骤在于以数据驱动和患者特异性的方式估算肿瘤细胞的分布(Lipková等,2019;Unkelbach等,2014;Rockne等,2010, 2015, 2019)。GBM生长的数学模型在预测肿瘤进展和指导个性化治疗决策中发挥着重要作用(Baldock等,2013;Lipková等,2019)。反应-扩散型偏微分方程(PDE)通常用于建模GBM的生长过程,以描述肿瘤细胞密度的时空演化,反映其增殖和浸润行为(Harpold等,2007)。然而,将这些模型应用于临床需要从临床数据中估算患者特异性的PDE参数,这是一个具有挑战性的逆问题。
方法创新 本研究提出了一种基于物理信息神经网络(Physics-Informed Neural Networks, PINNs)的方法,用于从单次3D结构MRI扫描中估算GBM生长的反应-扩散PDE模型的患者特异性参数。PINNs通过自动微分技术将PDE和数据嵌入损失函数,结合数学模型与数据驱动的学习过程。这种方法具有以下创新点:提出了一种简单的程序,用于估算患者特异性的无量纲特征参数,解决单时间点推断的局限性。设计了一个两阶段训练流程:在预训练阶段,利用患者特异性的无量纲参数训练PINN学习PDE的特征解;在微调阶段,训练PINN以学习患者特异性参数。引入弥散域方法处理复杂的脑部几何形状。
结果与局限性 该方法在合成数据和患者数据上进行了验证。通过参数估计,能够预测肿瘤细胞密度分布,辅助个性化放疗计划设计。验证结果表明,PINN能够高效、有效地解决PDE参数估计问题,特别是在有限时间点的临床数据中。然而,目前的研究作为概念验证,数据规模有限,且模型未包含不确定性量化。此外,本方法基于简化模型,与其他计算方法的优劣比较将在第3.3节详细讨论。文章结构 第2节介绍方法的组成,包括肿瘤生长的数学模型(第2.1节)、参数估计过程的工作流(第2.2节)以及PINN训练使用的损失函数(第2.3节)。第3节展示研究结果,首先在合成数据上验证方法(第3.1节),然后应用于患者数据(第3.2节),并在第3.3节讨论方法的优缺点。第4节总结研究结论。附录中提供了更多技术细节和结果。
Abatract
摘要
Predicting the infiltration of Glioblastoma (GBM) from medical MRI scans is crucial for understanding tumorgrowth dynamics and designing personalized radiotherapy treatment plans. Mathematical models of GBMgrowth can complement the data in the prediction of spatial distributions of tumor cells. However, this requiresestimating patient-specific parameters of the model from clinical data, which is a challenging inverse problemdue to limited temporal data and the limited time between imaging and diagnosis. This work proposes a methodthat uses Physics-Informed Neural Networks (PINNs) to estimate patient-specific parameters of a reaction–diffusion partial differential equation (PDE) model of GBM growth from a single 3D structural MRI snapshot.PINNs embed both the data and the PDE into a loss function, thus integrating theory and data. Key innovationsinclude the identification and estimation of characteristic non-dimensional parameters, a pre-training step thatutilizes the non-dimensional parameters and a fine-tuning step to determine the patient specific parameters.Additionally, the diffuse-domain method is employed to handle the complex brain geometry within the PINNframework. The method is validated on both synthetic and patient datasets, showing promise for personalizedGBM treatment through parametric inference within clinically relevant timeframes.
从医学磁共振成像(MRI)扫描中预测胶质母细胞瘤(Glioblastoma, GBM)的浸润情况对于理解肿瘤生长动态及设计个性化放射治疗计划至关重要。GBM生长的数学模型可以补充数据,用于预测肿瘤细胞的空间分布。然而,这需要从临床数据中估计患者特异性的模型参数,这是一个具有挑战性的逆问题,因为时间数据有限且成像与诊断之间的时间较短。本研究提出了一种方法,利用物理信息神经网络(Physics-Informed Neural Networks, PINNs)从单次3D结构MRI扫描中估计GBM生长反应扩散偏微分方程(PDE)模型的患者特异性参数。PINNs将数据和PDE嵌入到一个损失函数中,从而实现理论与数据的结合。关键创新包括特征无量纲参数的识别与估计、利用无量纲参数的预训练步骤以及用于确定患者特异性参数的微调步骤。此外,该方法在PINN框架内采用弥散域方法(diffuse-domain method)来处理复杂的大脑几何形状。该方法在合成数据和患者数据集上进行了验证,结果表明其在临床相关时间范围内通过参数推断实现个性化GBM治疗具有潜力。
Method
方法
2.1. Model2.1.1. Tumor model
We consider the Fisher–KPP PDE, a fundamental model that describes the spatio-temporal evolution of the normalized tumor celldensity 𝑢(𝐱, 𝑡) in a 3D domain 𝛺 consisting of white matter (WM) andgrey matter (GM) regions (Harpold et al., 2007; Swanson et al., 2000).The PDE, with Neumann boundary conditions, is given by{𝜕𝑢𝜕𝑡= 𝛁 ⋅ (D(𝐱)𝛁𝑢) 𝜌𝑢(1 − 𝑢) in 𝛺𝛁𝑢 ⋅ 𝐧 = 0 on 𝜕**𝛺(1)where 𝜌 [1/day] is the proliferation rate and D(𝐱) [mm2/day] is thediffusion tensor, and 𝐧 is the outward normal vector on the boundary𝜕𝛺*. We further assume that the diffusion is isotropic, and is a weightedsum of the diffusion coefficient in WM and GM, D(𝐱) = 𝐷𝑤𝑃w(𝐱) +𝐷𝑔𝑃g (𝐱), where 𝑃w, 𝑃g are the percentages of white and grey matter,and 𝐷𝑤, 𝐷𝑔 [mm2/day] are the diffusion coefficient in white and greymatter. We model heterogeneous diffusion by assuming 𝐷𝑤 = 𝑐𝐷𝑔with 𝑐 = 10 (Menze et al., 2011; Lipková et al., 2019; Swanson et al.,2000). For a review of this assumption and a comparison with thehomogeneous diffusion case (c = 1), see Appendix A.
2.1. 模型2.1.1. 肿瘤模型
我们采用Fisher–KPP偏微分方程(PDE),这一基本模型描述了归一化肿瘤细胞密度 𝑢(𝐱, 𝑡) 在一个由白质(WM)和灰质(GM)区域组成的三维域 𝛺 中的时空演化(Harpold等,2007;Swanson等,2000)。该PDE具有Neumann边界条件,表达式如下:∂u∂t=∇⋅(D(x)∇u)+ρu(1−u),在 Ω∇u⋅n=0,在 ∂Ω(1)\begin{aligned} \frac{\partial u}{\partial t} &= \nabla \cdot (D(\mathbf{x}) \nabla u) + \rho u(1 - u), \quad \text{在} \, \Omega \ \nabla u \cdot \mathbf{n} &= 0, \quad \text{在} \, \partial \Omega \end{aligned} \tag{1}其中,𝜌(单位:[1/天])为增殖率,D(𝐱)(单位:[mm²/天])为扩散张量,𝐧 为边界 𝜕𝛺 上的外法向量。我们进一步假设扩散是各向同性的,并表示为白质和灰质扩散系数的加权和:D(x)=DwPw(x)+DgPg(x),D(\mathbf{x}) = D_w P_w(\mathbf{x}) + D_g P_g(\mathbf{x}),其中,𝑃w 和 𝑃g 分别为白质和灰质的百分比,𝐷𝑤 和 𝐷**𝑔(单位:[mm²/天])为白质和灰质中的扩散系数。为了表示异质扩散,我们假设 𝐷𝑤 = 𝑐𝐷𝑔,其中 𝑐 = 10(Menze等,2011;Lipková等,2019;Swanson等,2000)。关于这一假设及其与均质扩散情况(𝑐 = 1)的比较,详见附录A。
Conclusion
结论
We presented a method employing Physics-Informed Neural Networks (PINNs) to estimate patient-specific parameters of a reaction–diffusion PDE model for the growth of GBM tumors from a singlesnapshot of structural MRI scans. We applied a simple procedure toestimate patient-specific characteristic parameters of the PDE modelusing a 1D model in spherically symmetric geometries and a grid-searchprocedure. The characteristic parameters allowed us to scale the PDE tolearn parameters that are close to unity, and helped us to pre-train thePINN to learn a characteristic solution before fine-tuning the networkwith patient data to estimate the patient-specific parameters, leadingto a more efficient method. Verified on synthetic and patient datasets,the results presented here provide a proof-of-concept that PINNs holdgreat promise for combining medical images and biophysical modelsfor patient-specific tumor growth prediction and treatment planning.
我们提出了一种采用物理信息神经网络的方法利用物理信息神经网络(PINNs)来估算患者特定的反应参数用于从单个细胞开始的胶质母细胞瘤(GBM)肿瘤生长的扩散偏微分方程模型结构磁共振成像(MRI)扫描的快照。我们应用了一个简单的程序来估计偏微分方程模型中患者的特定特征参数在球对称几何中使用一维模型和网格搜索过程。这些特征参数使我们能够对偏微分方程进行缩放。学习接近于 1 的参数,并帮助我们对模型进行预训练在对网络进行微调之前,使用 PINN 学习一个特征解利用患者数据来估算患者特定的参数,从而一种更高效的方法。在合成数据集和患者数据集上得到验证,这里展示的结果证明了物理信息神经网络(PINNs)具有可行性。将医学影像与生物物理模型相结合具有巨大的前景。用于患者特异性的肿瘤生长预测和治疗规划。
Results
结果
We start by presenting an overview of the results and our findings.In this work we use 3 different datasets, including data from 24patients, to test and validate our approach:
• Synthetically-generated data, denoted as S1–S8: We specify theground truth (GT) parameters, solve the PDE by the FDM to obtain the cell density, add spatially correlated noise to the density,and generate synthetic segmentations and FET distributions.
• Data from 8 patients (P1–P8), primary tumors and first detectedrecurrence, from Lipková et al. (2019). All the patients have TCand WT segmentations at recurrence.
• Data from 16 patients (Q1–Q16), primary and first detected recurrence, from the Klinikum Rechts Der Isar repository. At recurrence, patients Q1–Q3 have both TC and WT segmentations, theothers only have TC segmentation.We test parameter estimation using segmentations data and FETPET (denoted as FET+SEG), and using segmentations alone (denoted as*SEG). The difference between the two lies in the loss functions used inthe fine-tuning stage: FET+SEG** includes the FET loss FET, in additionto the segmentation loss SEG.We demonstrate that using segmentation alone achieves resultscomparable to those using segmentation and FET, in contrast to theresults in Lipková et al. (2019) where FET was needed to more accurately determine spatial distributions of the cells, particularly near thetumor center. This finding is noteworthy as FET-PET data is not widelyavailable from the clinic, thereby accentuating the practicality of ourapproach.Furthermore, we examine two methods to predict cell density afterfine-tuning: 𝑢 𝐹𝐷𝑀 , derived from solving the PDE with estimated parameters using the FDM, and 𝑢 𝑃 𝐼𝑁𝑁 , obtained by evaluating the PINN.We show that 𝑢 𝐹𝐷𝑀 is more accurate in solving the PDE as 𝑢 𝑃 𝐼𝑁𝑁 isinfluenced by the noisy data via the loss function. Additionally, theFDM can be used to solve the PDE to any non-dimensional time. However, extending the PDE solution to future times with the PINN requiresre-sampling and extending the collocation points, and retraining thenetwork with the PDE loss, which tends to be more time consuming.
我们首先概述研究结果和主要发现。
在本研究中,我们使用了三个不同的数据集,包括来自24名患者的数据,测试和验证我们的方法:Synthetically-generated data (S1–S8): 通过设定真实值(GT)参数,利用有限差分法(FDM)求解偏微分方程(PDE)以获得细胞密度,再向密度中添加空间相关噪声,并生成合成分割和FET分布。
8名患者的数据(P1–P8): 来源于Lipková等人(2019年)的研究,包含原发肿瘤和首次检测到的复发。所有患者在复发时均有肿瘤核心(TC)和全肿瘤(WT)分割。16名患者的数据(Q1–Q16): 来源于Klinikum Rechts Der Isar数据库,包括原发肿瘤和首次检测到的复发。在复发时,Q1–Q3患者有TC和WT分割,其余患者仅有TC分割。我们分别测试了基于分割数据和FET PET数据(FET+SEG)以及仅基于分割数据(SEG)的参数估计方法。两者的区别在于微调阶段的损失函数:FET+SEG在分割损失(SEG)的基础上额外引入了FET损失(FET)。我们发现,仅使用分割数据即可获得与同时使用分割和FET数据相当的结果,这与Lipková等人(2019年)的结果相反。当时,FET数据被认为是更准确确定细胞空间分布(尤其是肿瘤中心附近)的必要条件。这一发现尤为重要,因为FET-PET数据在临床中并不广泛可得,从而突出了我们方法的实用性。此外,我们探讨了微调后预测细胞密度的两种方法:
通过FDM求解PDE得到的𝑢𝐹𝐷𝑀:基于估计参数使用有限差分法。通过PINN评估得到的𝑢𝑃𝐼𝑁𝑁:由PINN通过损失函数对含噪声数据的评估得到。研究表明,𝑢 𝐹𝐷𝑀 在求解PDE方面更为精确,而𝑢 𝑃𝐼𝑁𝑁 会受到噪声数据的影响。此外,FDM可以在任意无量纲时间求解PDE,而通过PINN扩展PDE解到未来时间需要重新采样并扩展配点,同时用PDE损失重新训练网络,这通常更耗时。
Figure
图

Fig. 1. Challenges and method of our framework to handle the polyps segmentation via using the colonoscopy images. From (a) to (b), they are preliminary work ICGNet and improved method UM-Net, the new challenges of our tasks, respectively.
图 1. 我们框架在处理基于结肠镜图像的息肉分割任务中的挑战与方法。从(a)到(b),分别展示了前期工作ICGNet、改进方法UM-Net,以及任务中面临的新挑战。

Fig. 2. Workflow for patient-specific parameter estimation via PINN. I. Preprocessing: Register the brain atlas to the T1Gd patient scan. Solve the Cahn–Hilliard equation toacquire the geometry. Compute centers and radii of Tumor Core (TC) and Whole Tumor (WT) segmentations (𝑅TC seg and 𝑅W seg T ). II. Grid Search: In a spherically symmetric geometry,use a grid search algorithm to identify patient-specific characteristic values of ̄𝐷∕ ̄𝜌 and ̄𝐿 such that the radii derived from the PDE solution are close to 𝑅TC seg and 𝑅W seg T . III.*Pre-training: Solve the PDE using a Finite Difference Method (FDM) with the patient-specific characteristic parameters (and 𝜇 = 𝜇 = 1) in the registered atlas geometry toobtain a characteristic solution ̄𝑢 𝐹𝐷𝑀 . Train the PINN to solve the PDE using ̄𝑢 𝐹𝐷𝑀 as data. IV. Fine-Tuning: Use the segmentation data to fine-tune the PINN and learn thepatient specific parameters 𝜇 and 𝜇. These estimated parameters are used for tumor cell density predictions.
图2. 基于PINN的患者特异性参数估计工作流程。 I. 预处理: 将脑图谱配准至患者的T1Gd扫描。求解Cahn–Hilliard方程以获得几何信息。计算肿瘤核心(TC)和全肿瘤(WT)分割的中心和半径(𝑅TC seg 和 𝑅WT seg)。 II. 网格搜索: 在球对称几何中,使用网格搜索算法识别患者特异性的̄**𝐷∕̄𝜌和̄𝐿的特征值,使得PDE解得出的半径接近𝑅TC seg 和 𝑅WT seg。 III. 预训练: 使用患者特异性特征参数(且𝜇 = = 1)在配准的图谱几何中,通过有限差分法(FDM)求解PDE,得到特征解̄。利用̄作为数据训练PINN以求解PDE。 IV. 微调: 使用分割数据微调PINN,学习患者特异性的参数𝜇和𝜇。这些估计参数用于肿瘤细胞密度的预测。

Fig. 3. Validation using synthetic data. Row 1: (a)–(d). ground truth (GT) data; Row2: (e)–(h). Training data based on GT data with spatially correlated noise; Row 3🙁i)–(l). Parameter estimation using noisy, synthetic FET+SEG data and predictions byevaluating the PINN solution, 𝑢 𝑃 𝐼𝑁𝑁 ; Row 4: (m)–(p). Parameter estimation usingnoisy FET+SEG data and predictions using the FDM solution of the PDE, 𝑢 𝐹𝐷𝑀 , withinferred parameters; Row 5: (q)–(t). Parameter estimation using only the noisy SEGdata and predictions using 𝑢 𝐹𝐷𝑀 . (t): Comparison of contours at 1%, 25%, 50%, and75% between 𝑢 𝐹𝐷𝑀 (solid) and GT 𝑢 (dotted). Column 1: 3D isosurfaces of tumor celldensity at 1% and 𝑦 WT ; Column 2: Cell densities; Column 3: Synthetic segmentationsmimicking TC and WT data; Column 4: Synthetic FET-PET distributions. Further, (k),(o) and (s) show comparisons of predicted segmentations (lines–dashed, solid) withGT segmentations (filled). Comparing rows 3 and 4, 𝑢 𝑃 𝐼𝑁𝑁 is less accurate than 𝑢 𝐹𝐷𝑀as a solution of the PDE with the inferred parameters because 𝑢 𝑃 𝐼𝑁𝑁 is more stronglyinfluenced by the noisy data. Notably, the estimated cell densities from the 𝑢 𝐹𝐷𝑀 usingFET+SEG and SEG in rows 4 and 5, respectively, are very similar and yield accurateapproximations of the GT data.
图3. 使用合成数据进行验证。第1行 (a)–(d): 真值(GT)数据。第2行 (e)–(h): 基于GT数据添加空间相关噪声的训练数据。第3行 (i)–(l): 使用含噪FET+SEG数据进行参数估计,并通过评估PINN解(𝑢 𝑃𝐼𝑁𝑁)进行预测。第4行 (m)–(p): 使用含噪FET+SEG数据进行参数估计,并通过PDE的FDM解(𝑢 𝐹𝐷𝑀)及推断的参数进行预测。第5行 (q)–(t): 仅使用含噪SEG数据进行参数估计,并通过𝑢 𝐹𝐷𝑀进行预测。(t):比较𝑢 𝐹𝐷𝑀(实线)和GT 𝑢(虚线)在1%、25%、50%和75%处的等值线。第1列: 肿瘤细胞密度在1%和𝑦 WT处的3D等值面。第2列: 细胞密度。第3列: 模拟TC和WT数据的合成分割。第4列: 模拟FET-PET分布。
此外,(k)、(o) 和 (s) 显示了预测分割(虚线、实线)与GT分割(填充区域)的比较。比较第3行和第4行可以看出,作为基于推断参数的PDE解,𝑢 𝑃𝐼𝑁𝑁比𝑢 𝐹𝐷𝑀的准确性更差,因为𝑢 𝑃𝐼𝑁𝑁更容易受到含噪数据的影响。值得注意的是,第4行和第5行的𝑢 𝐹𝐷𝑀从FET+SEG和SEG数据中估计的细胞密度非常相似,并能准确逼近GT数据。

Fig. 4. Predicted tumor morphologies at times different from that of training data.Morphologies are shown at the normalized times 𝑡̄ = 0.6, 0.8, 1.0, 1.2 and are obtainedusing 𝑢 𝐹𝐷𝑀 with parameters inferred from the synthetic data in Fig. 3. Only SEG data isused for inference and the training data corresponds to the normalized time 𝑡̄ = 1. Row1: 3D isosurfaces of 𝑢 𝐹𝐷𝑀 at 1% and 30% Row 2: Comparison of predicted contours(solid; 1%, 25%, 50% and 75%) with GT (dotted)
图4. 在与训练数据不同时间点预测的肿瘤形态。
肿瘤形态显示在归一化时间𝑡̄ = 0.6、0.8、1.0、1.2处,并通过使用图3中的合成数据推断参数得到的𝑢 𝐹𝐷𝑀计算。推断仅使用SEG数据,训练数据对应归一化时间𝑡̄ = 1。第1行: 𝑢 𝐹𝐷𝑀在1%和30%处的3D等值面。第2行: 预测等值线(实线;1%、25%、50%和75%)与GT(虚线)的比较。

Fig. 5. Predicted patient-specific tumor morphologies, cell densities and FET-PETdistributions from Patient 5. Row 1: Medical images: (a) T1Gd; (b) FLAIR; © Postprocessed FET-PET (see Section 2.1.4); (d) Original FET-PET data. Row 2: 𝑢 𝐹𝐷𝑀predictions using FET+SEG data. Row 3: 𝑢 𝐹𝐷𝑀 predictions using SEG data only. (e)and (i): Predicted cell density distributions from 𝑢 𝐹𝐷𝑀 together with boundaries of thesegmentations (curves) from the MRI images. (f) and (j): Comparisons of the contours of𝑢 𝐹𝐷𝑀 at the inferred segmentation thresholds (curves) with MRI segmentations (filled).Margins for CTV RTOG (green) and CTV P (blue); (g) predicted FET-PET distribution.(h) 3D visualization of 1% and 𝑢 W 𝑐 T isosurfaces. (k) Comparison of 1%, 𝑢 W 𝑐 T , and 𝑢 TC 𝑐contours of 𝑢 𝐹𝐷𝑀 (solid) and 𝑢 𝑃 𝐼𝑁𝑁 (dashed). (l) Predicted cell density distributionsfrom 𝑢 𝐹𝐷𝑀 on the registered atlas, together with 𝜕𝛺 (orange).
图5. 基于患者5的预测结果,包括患者特异性的肿瘤形态、细胞密度及FET-PET分布。第1行:医学图像(a) T1Gd;(b) FLAIR;© 经过后处理的FET-PET(见2.1.4节);(d) 原始FET-PET数据。第2行: 使用FET+SEG数据的𝑢 𝐹𝐷𝑀预测结果。第3行: 仅使用SEG数据的𝑢 𝐹𝐷𝑀预测结果。(e) 和 (i):从𝑢 𝐹𝐷𝑀预测的细胞密度分布,并标出MRI图像中的分割边界(曲线)。(f) 和 (j):𝑢 𝐹𝐷𝑀在推断分割阈值处的等值线(曲线)与MRI分割(填充区域)的比较。包括CTV RTOG(绿色)和CTV P(蓝色)的边界。(g):预测的FET-PET分布。(h):1%和𝑢 W 𝑐 T等值面的3D可视化。(k):𝑢 𝐹𝐷𝑀(实线)和𝑢 𝑃 𝐼𝑁𝑁(虚线)在1%、𝑢 W 𝑐 T 和𝑢 TC 𝑐等值线的比较。(l):基于配准图谱的𝑢 𝐹𝐷𝑀预测细胞密度分布,并标出𝜕𝛺(橙色)。

Fig. 6. Predicted dynamics of tumor from Patient 5 using the FDM at normalized times𝑡̄ = 0.6, 0.8, 1.0, 1.2. The data is provided at 𝑡̄ = 1. The 3D isosurfaces of 𝑢 𝐹𝐷𝑀 at 1%and predicted 𝑢 W 𝑐 T are shown.
图6. 使用有限差分法(FDM)预测患者5肿瘤的动态变化,归一化时间为𝑡̄ = 0.6、0.8、1.0、1.2。
在时间𝑡̄ = 1提供数据。显示了𝑢 𝐹𝐷𝑀在1%处的3D等值面以及预测的𝑢 W 𝑐 T等值面。

Fig. 7. Parameter estimation results for patients P1–P8 using SEG. (A) Pre-operative T1Gd. (B) Pre-operative FLAIR. © Superposition of predicted tumor cell density 𝑢 𝐹𝐷𝑀 onactual segmentations: WT (yellow line) and TC (red line). (D) Superposition of predicted tumor cell density 𝑢 𝐹𝐷𝑀 on registered atlas with 𝜕𝛺 (orange line). (E) Overlap of inferredsegmentations: 𝑢 W 𝑐 T (yellow line) and 𝑢 TC 𝑐 (red line) on actual segmentations: WT (beige fill) and TC (pink fill); Margins for CTV RTOG (green) and CTV P (blue). (F) Tumor recurrence,compared with margins for CTV RTOG (green) and CTV P (blue). (G) 3D reconstructions of CTV P and 𝑢 W 𝑐 T isosurfaces. On average, pre-training took 37.9 (± 5.0) minutes, whilefine-tuning was completed in 4.5 (± 0.1) minutes. Results using FET+SEG are shown in Fig. I.16
图7. 使用SEG进行患者P1–P8的参数估计结果。(A): 术前T1Gd图像。(B): 术前FLAIR图像。©: 预测的肿瘤细胞密度𝑢 𝐹𝐷𝑀叠加在实际分割上:全肿瘤(WT,黄色线)和肿瘤核心(TC,红色线)。(D): 预测的肿瘤细胞密度𝑢 𝐹𝐷𝑀叠加在配准图谱上,并显示𝜕𝛺(橙色线)。(E): 推断分割结果的重叠:𝑢 W 𝑐 T(黄色线)和𝑢 TC 𝑐(红色线)与实际分割结果的对比:全肿瘤(WT,米色填充)和肿瘤核心(TC,粉色填充);同时显示CTV RTOG(绿色)和CTV P(蓝色)的边界。(F): 肿瘤复发与CTV RTOG(绿色)和CTV P(蓝色)边界的对比。(G): CTV P和𝑢 W 𝑐 T等值面的3D重建。平均来看,预训练耗时37.9(± 5.0)分钟,微调耗时4.5(± 0.1)分钟。使用FET+SEG的数据的结果见图I.16。

Fig. 8. Parameter Estimation Results for Patients Q1–Q8 using SEG. Recurrence results for Q1–Q3 are shown in Appendix I Fig . I.20. Legends are the same as 7. Results usingFET+SEG are shown in Appendix I Fig. I.18
图8. 使用SEG对患者Q1–Q8的参数估计结果。
患者Q1–Q3的复发结果见附录I图I.20。图例与图7相同。使用FET+SEG的数据的结果见附录I图I.18。

Fig. 9. Parameter Estimation Results for Patients Q9–Q16 using SEG. Legends are the same as 7. Results using FET+SEG are shown in Appendix I Fig. I.19.
图。9.使用 SEG 对患者 Q9-Q16 进行参数估计的结果。图例与图 7 相同。使用 FET + SEG 的结果见附录 I 图 I.19。

Fig. A.10. Comparison of the effect of using heterogeneous (c = 10) and homogeneous(𝑐 = 1) diffusion. Assuming homogeneous diffusion coefficient leads to sphericalcontours and larger infiltration.
图 A.10. 比较异质扩散(c = 10)与均质扩散(c = 1)的效果。假设均质扩散系数会导致扩散轮廓呈球形并产生更大的浸润范围。

Fig. B.11. Estimated tumor cell density for P5 using SEG on the registered atlason the patient geometry (T1Gd, left column) and the registered atlas geometry (rightcolumn) using affine registration (top row) and diffeomorphic registration (bottomrow). Diffeomorphic registration leads to better results near the ventricles.
图 B.11.在患者 P5 的几何结构上使用 SEG 和配准的模板(T1Gd,左列),以及在配准模板几何结构(右列)上,分别采用仿射配准(上行)和形变配准(下行)估算的肿瘤细胞密度。形变配准在靠近脑室区域的结果更优。

Fig. E.12. Example of training loss for patient P5 with FET+SEG. The left figure showsthe training loss for pre-training with residual loss and 𝑢 𝐹𝐷𝑀 . The right figure showsthe training loss for fine-tuning with segmentation loss and PET loss. The weights arechosen such that the two loss magnitudes are similar.
图 E.12.患者 P5 在 FET+SEG 条件下的训练损失示例。左图显示了基于残差损失和 𝑢 𝐹𝐷𝑀 的预训练损失;右图显示了基于分割损失和 PET 损失的微调训练损失。权重的选择使两种损失的量级相似。

Fig. F.13. The distribution of collocation points for the residual loss in the radialdirection is shown as a scatter plot with ̄𝑢 𝐹𝐷𝑀 and r (radii of 𝐱 r ) and color-coded bytime spanning from 0 to 1. The PDE solution is concentrated at the center where thereis a larger gradient at early times, and the collocation points are densely sampledat the center and at early times. Inset (a) shows a histogram of r (normalized to aprobability density function), highlighting that due to near-uniform distribution in polarcoordinates, 𝐱 r is denser at the center. Inset (b) shows a histogram of time (normalizedas a probability density function), indicating a denser sampling in the earlier timeperiods.
图 F.13.用于残差损失的径向方向搭配点分布显示为散点图,其中 ̄𝑢 𝐹𝐷𝑀 和 r(𝐱r_r 的半径)按时间从 0 到 1 进行颜色编码。偏微分方程(PDE)的解集中于中心区域,早期时间内梯度较大,搭配点在中心和早期时间段内被密集采样。插图 (a) 为 r 的直方图(归一化为概率密度函数),突出由于极坐标中近似均匀分布,𝐱r_r 在中心区域更加密集。插图 (b) 为时间的直方图(归一化为概率密度函数),表明采样在早期时间段内更为密集。

Fig. G.14. Illustration of spatially correlated noise, as employed in Fig. 5. Noise isproduced by sampling from a Gaussian distribution (mean 0 and standard deviation 2)at each pixel and subsequently applying a Gaussian filter of size 13.
图 G.14.空间相关噪声的示意图,如图 5 所示。噪声通过在每个像素处从均值为 0、标准差为 2 的高斯分布中采样生成,随后应用大小为 13 的高斯滤波器进行处理。

Fig. I.15. Comparison of predicted tumor cell densities 𝑢 𝐹𝐷𝑀 and 𝑢 𝑃 𝐼𝑁𝑁 for patientP5 using SEG data, as supplement to Fig. 5. 𝑢 𝑃 𝐼𝑁𝑁 is influenced by the noise
图 I.15.患者 P5 使用 SEG 数据的预测肿瘤细胞密度 𝑢 𝐹𝐷𝑀 和 𝑢 𝑃 𝐼𝑁𝑁 的比较,作为图 5 的补充。𝑢 𝑃 𝐼𝑁𝑁 受到噪声的影响。

Fig. I.16. Parameter estimation results for patients P1–P8 using FET+SEG. Pre-operative T1Gd and FLAIR are identical to Fig. 7. (A) FET signal. (B) Pre-processed PET bysubtracting the background average and normalized to [0,1]. © Superimposition of predicted tumor cell density 𝑢 𝐹𝐷𝑀 on actual segmentations: T1Gd (yellow line) and FLAIR(red line). (D) Predicted FET signal. (E) Overlap of inferred segmentations: 𝑢 W 𝑐 T (yellow line) and 𝑢 TC 𝑐 (red line) on actual segmentations: WT (beige fill) and TC (pink fill); Marginsfor CTV RTOG (green) and CTV P (blue). (F) Tumor recurrence, compared with margins for CTV RTOG (green) and CTV P (blue). (G) 3D reconstructions of CTV P and 𝑢 W 𝑐 T isosurfaces.
图 I.16.患者 P1–P8 使用 FET+SEG 的参数估计结果。术前 T1Gd 和 FLAIR 图像与图 7 相同。(A) FET 信号。(B) 背景均值减法预处理并归一化至 [0,1] 的 PET 图像。© 预测的肿瘤细胞密度 𝑢 𝐹𝐷𝑀 与实际分割图的叠加:T1Gd(黄色线)和 FLAIR(红色线)。(D) 预测的 FET 信号。(E) 推断的分割结果与实际分割的重叠:𝑢 W 𝑐 T(黄色线)和 𝑢 TC 𝑐(红色线)与实际分割结果:WT(米色填充)和 TC(粉色填充);CTV RTOG(绿色)和 CTV P(蓝色)的边界。(F) 肿瘤复发,与 CTV RTOG(绿色)和 CTV P(蓝色)边界进行比较。(G) CTV P 和 𝑢 W 𝑐 T 等值面的三维重建。

Fig. I.17. Results for patients P1–P8 using characteristic parameters without fine-tuning. For all cases, 𝜇 = 𝜇 = 1, 𝑚 = 1, 𝐴 = 0, 𝑢 TC 𝑐 = 0.6, 𝑢 W 𝑐 T = 0.35. (a) Pre-operative T1Gd.(b) Pre-operative FLAIR. © Superimposition of predicted tumor cell density 𝑢 𝐹𝐷𝑀 on actual segmentations: WT (yellow line) and TC (red line). (d) Predicted FET signal. (d)Overlap of inferred segmentations: 𝑢 W 𝑐 T (yellow line) and 𝑢 TC 𝑐 (red line) on actual segmentations: WT (beige fill) and TC (pink fill); Margins for CTV RTOG (green) and CTV P (glue,1% contour of 𝑢 𝐹𝐷𝑀 ). (e) Tumor recurrence, compared with margins for CTV RTOG (green) and CTV P (blue). (f) 3D reconstructions of CTV P and 𝑢 W 𝑐 T isosurfaces
图 I.17.患者 P1–P8 在未进行微调的情况下,使用特征参数的结果。所有病例中参数为 𝜇 = 𝜇 = 1,𝑚 = 1,𝐴 = 0,𝑢 TC 𝑐 = 0.6,𝑢 W 𝑐 T = 0.35。
(a) 术前 T1Gd 图像。(b) 术前 FLAIR 图像。© 预测的肿瘤细胞密度 𝑢 𝐹𝐷𝑀 与实际分割结果的叠加:WT(黄色线)和 TC(红色线)。(d) 预测的 FET 信号。(e) 推断分割结果与实际分割的重叠:𝑢 W 𝑐 T(黄色线)和 𝑢 TC 𝑐(红色线)与实际分割结果:WT(米色填充)和 TC(粉色填充);CTV RTOG(绿色)和 CTV P(蓝色)边界;𝑢 𝐹𝐷𝑀 的 1% 等值线。(f) 肿瘤复发,与 CTV RTOG(绿色)和 CTV P(蓝色)边界的比较。(g) CTV P 和 𝑢 W 𝑐 T 等值面的三维重建。

Fig. I.18. Parameter Estimation Results for Patients Q1–Q8 using FET+SEG. Results with SEG is shown in Fig. I.18.
图 I.18.患者 Q1–Q8 使用 FET+SEG 的参数估计结果。SEG 的结果见图 I.18。

Fig. I.19. Parameter Estimation Results for Patients Q9–Q16 using FET+SEG. Results with SEG is shown in Fig. 8.
图 I.19.患者 Q9–Q16 使用 FET+SEG 的参数估计结果。SEG 的结果见图 8。

Fig. I.20. Recurrent tumors from patients Q1–Q3 and PDE model predictions usingSEG, as supplement to Fig. 9
图 I.20.患者 Q1–Q3 的复发性肿瘤以及 PDE 模型基于 SEG 的预测结果,作为图 9 的补充。

Fig. I.21. Comparison of RTOG CTV (green) with Personalized CTV FET+SEG (blue)for patient Q13 over (A) pre-operative tumor and (B) recurrent tumor. Overlap ofinferred segmentations 𝑢 W 𝑐 T (yellow line) and 𝑢 TC 𝑐 (red line) on actual segmentations:WT (beige fill) and TC (pink fill); Margins for CTV RTOG (green) and CTV P (blue)
图 I.21.患者 Q13 的 RTOG CTV(绿色)与个性化 CTV FET+SEG(蓝色)的比较:(A) 术前肿瘤。
(B) 复发肿瘤。推断分割结果的重叠:𝑢 W 𝑐 T(黄色线)和 𝑢 TC 𝑐(红色线)与实际分割结果的重叠:WT(米色填充)和 TC(粉色填充);CTV RTOG(绿色)和 CTV P(蓝色)的边界。

Fig. J.22. Box plot of the estimated tumor growth parameters 𝜇∕0.1 and 𝜇∕10for all 24 patients, including the characteristic parameters (labeled as Char) and thefinal parameters after fine-tuning with SEG and FET+SEG data.
图 J.22.所有 24 名患者的肿瘤生长参数 𝜇∕0.1 和 𝜇∕10 的箱线图,包括特征参数(标记为 Char)以及使用 SEG 和 FET+SEG 数据微调后的最终参数。

Fig. J.23. Box plot of tumor core (TC) and whole tumor (WT) DICE scores andcorrelation with FET signal for all 24 patients using the characteristic solution (labeledas Char), or the solution after fine-tuning with SEG with FET+SEG data. .
图 J.23.所有 24 名患者的肿瘤核心区(TC)和全肿瘤区(WT)DICE 得分及与 FET 信号相关性的箱线图,分别展示特征解(标记为 Char)和使用 SEG 与 FET+SEG 数据微调后的解。

Fig. K.24. Correlation between FET signal and solidity of the FET region. Thecorrelation is 0.757 with 𝑝-value 1.8e−5. Ring-like FET signals has solidity valueslower than 1, indicative of a central void, and is related to lower correlation betweenpredicted cell densities and FET signals.
图 K.24.FET 信号与 FET 区域实心度之间的相关性。相关系数为 0.757,p-值为 1.8e−5。环状 FET 信号的实心度值低于 1,表明存在中心空隙,并与预测细胞密度和 FET 信号之间的较低相关性相关。
Table
表

Table 1Average and standard deviation of DICE scores and correlation with FET signal for all24 patients using characteristic parameters, or parameters obtained by fine-tuning withSEG with FET+SEG data. Fine-Tuning leads to better results
表1使用特征参数或通过SEG和FET+SEG数据微调获得的参数对所有24名患者的DICE得分平均值及标准差,以及与FET信号的相关性。结果显示,微调能够取得更优的结果。

Table 2Comparison of RTOG CTVs with personalized CTVs (1% isosurface of predicted tumor cell density) from different parameter estimation methods: Lipkováet al. (2019), FET+SEG, and SEG: (a) Relative volume with respect to RTOG CTV. (b) Efficiency, the percentage of WT at the first detected recurrencethat is covered by the CTV, see Eq. (20). © Ratio of efficiency over relative volume. In general, the personalized CTVs from Lipková et al. (2019),FET+SEG, and SEG present reduced or similar irradiation volumes while maintaining efficiency comparable to RTOG CTV.
表2对比RTOG临床靶区(CTV)与不同参数估计方法所得个性化CTV(预测肿瘤细胞密度1%等值面)的结果:Lipková等人(2019)、FET+SEG和SEG。
(a): 相对于RTOG CTV的体积比例。(b): 效率,即首次检测到复发的全肿瘤(WT)被CTV覆盖的百分比(见公式(20))。©: 效率与相对体积的比值。
总体而言,Lipková等人(2019)、FET+SEG和SEG所得个性化CTV在辐射体积上有所减少或相近,同时保持与RTOG CTV相当的效率。

Table A.3Comparison of the performance metrics for heterogeneous (𝑐 = 10) and homogeneous (𝑐 = 1) diffusionmodels using SEG data for patients P1–P8. Metrics include DICE scores for total contrast-enhancing tumor(DICETC) and white matter (DICEWT), correlation with FET signal (corrFET), and efficiency-to-volume ratio(Eff/Vol) for recurrent tumors
表 A.3 使用 SEG 数据对患者 P1–P8 进行异质扩散模型(c = 10)和均质扩散模型(c = 1)的性能指标比较。指标包括总增强肿瘤的 DICE 得分(DICETC{TC})、白质的 DICE 得分(DICEWT{WT})、与 FET 信号的相关性(corrFET_{FET})以及复发肿瘤的效率体积比(Eff/Vol)。

Table B.4Mean and standard deviation of DICE scores for the tumor core (TC) and whole tumor (WT) regions, alongwith the correlation with the FET signal, for all 24 patients using diffeomorphic and affine registrationacross different methods (Char, SEG, FET+SEG).
表 B.4针对所有 24 名患者,肿瘤核心区(TC)和全肿瘤区(WT)DICE 得分的平均值和标准差,以及与 FET 信号的相关性,分别在形变配准(diffeomorphic registration)和仿射配准(affine registration)方法下的比较。

Table C.5Characteristic parameter estimation from synthetic data. Datasets S1, S3, S5, and S8 use 𝐱0 = (164, 116, 99) while S2, S4, S6, andS7 use 𝐱0 = (65, 70, 99). For this synthetic data, the estimated values for 𝜇 and 𝜇 are near 1, which is the targeted outcome.
表 C.5基于合成数据的特征参数估计。数据集 S1、S3、S5 和 S8 使用 𝐱₀ = (164, 116, 99),而 S2、S4、S6 和 S7 使用 𝐱₀ = (65, 70, 99)。对于这些合成数据,估计的 𝜇 和 𝜇 值接近 1,这是目标结果。
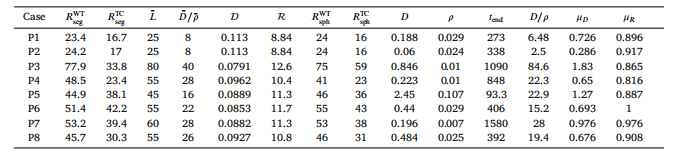
Table C.6Characteristic parameter estimation for patients P1–P8. Parameters 𝐷, 𝜌, and 𝑡 end are from Lipková et al. (2019) and used to compute𝜇 and 𝜇
表 C.6患者 P1–P8 的特征参数估计。参数 𝐷(扩散系数)、𝜌(增殖率)和 𝑡end_{end}(终止时间)来源于 Lipková 等人(2019),并用于相关计算。

Table C.7Characteristic parameter estimation for patients Q1–Q16
表 C.7患者 Q1–Q16 的特征参数估计。

Table D.8Baseline and perturbed simulation results for patient P5, showing characteristic parameters, predicted model
表 D.8患者 P5 的基线和扰动模拟结果,展示了特征参数和预测模型。

Table G.9Estimated parameters from the synthetic dataset using SEG and FET+SEG, compared with ground truth(GT) values
表 G.9基于合成数据集的估计参数,分别使用 SEG 和 FET+SEG,并与真实值(GT)进行比较。

Table H.10Statistics of absolute relative error (%) for 𝜇 and 𝜇 in the synthetic dataset (S1–S8) using varied datalosses for fine-tuning. u-t-all uses the ground truth cell density at residual collocation points over times in[0, 1], while u-t-end uses ground truth cell density at data collocation points at time 1. FET+SEG uses noisysegmentation and PET data. SEG uses noisy segmentation data only
表 H.10在合成数据集(S1–S8)中,针对 𝜇 和 𝜇 的绝对相对误差(%)统计,使用不同的数据损失进行微调。u-t-all 使用时间区间 [0, 1] 内残差搭配点的真实细胞密度。u-t-end 使用时间点 1 的数据搭配点的真实细胞密度。FET+SEG 使用带噪声的分割数据和 PET 数据。SEG 仅使用带噪声的分割数据。

Table I.11Average and standard deviation of DICE scores and correlation with FET signals for all24 patients using 𝑢 𝑃 𝐼𝑁𝑁 . The metrics are in general better than those using 𝑢 𝐹𝐷𝑀 (inTable 1), because 𝑢 𝑃 𝐼𝑁𝑁 might sacrifice fidelity to the PDE to fit the data.
表 I.11针对所有 24 名患者,使用 𝑢 𝑃 𝐼𝑁𝑁 的 DICE 得分和与 FET 信号相关性的平均值及标准差。相比于 𝑢 𝐹𝐷𝑀(见表 1),这些指标总体表现更佳,因为 𝑢 𝑃 𝐼𝑁𝑁 可能为了更好地拟合数据而牺牲了对偏微分方程(PDE)的保真性。

Table I.12Parameters estimated for patients P1–P8 using FET+SEG and SEG data, compared with results from Lipková et al. (2019)(∗ ).Parameters that are not included in the model are marked with ‘‘–’’. Metrics include DICE score for both WT and TCsegmentations, as well as correlation with the FET signal (see Appendix I)
表 I.12使用 FET+SEG 和 SEG 数据对患者 P1–P8 的参数估计,并与 Lipková 等人(2019)的结果(标记为 ∗)进行比较。未包含在模型中的参数以“–”标注。指标包括白质区(WT)和肿瘤核心区(TC)分割的 DICE 得分,以及与 FET 信号的相关性(详见附录 I)。

Table I.13Metrics for results using the characteristic parameters without fine-tuning. For all cases, 𝜇 = 𝜇 = 1,𝑚* = 1, 𝐴 = 0, 𝑢 TC 𝑐 = 0.6, 𝑢 W 𝑐 T = 0.35. Without finetuning, the metrics are not as good as the resultsin Table I.12.
表 I.13使用未微调特征参数的结果指标。所有病例的参数为 𝜇 = 𝜇 = 1,𝑚 = 1,𝐴 = 0,𝑢 TC 𝑐 = 0.6,𝑢 W 𝑐 T = 0.35。未进行微调时,这些指标的表现不如表 I.12 中的结果。
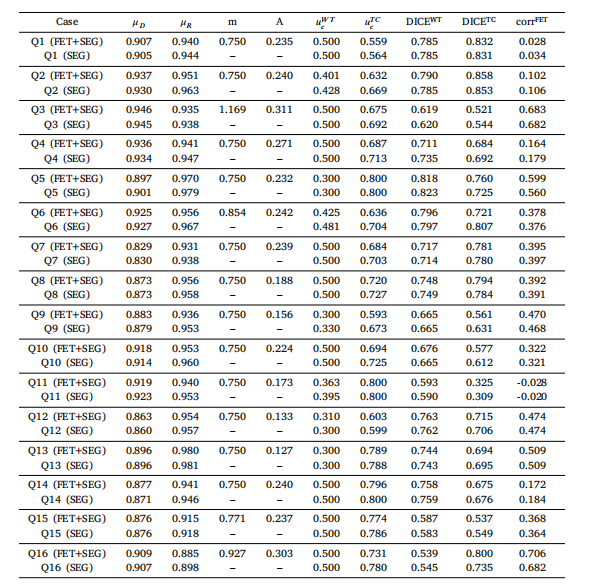
Table I.14Estimated parameters and metrics for Patients Q1–Q16, comparison between results using SEG and FET+SEGdata.、
表 I.14患者 Q1–Q16 的估计参数和指标,比较使用 SEG 和 FET+SEG 数据的结果。

Table I.15Comparison of RTOG CTVs with personalized CTVs (1% isosurface of predicted tumor cell density) from FET+SEG and SEG for Q1–Q13. (a)Relative volume with respect to RTOG CTV. (b) Efficiency, the percentage of TC at the first detected recurrence that is covered by the CTV(see text). © Ratio of efficiency over relative volume. In general, the personalized CTVs from FET+SEG and SEG present reduced or similarirradiation volumes while maintaining efficiency comparable to RTOG CTV
表 I.15比较患者 Q1–Q13 的 RTOG CTV 与个性化 CTV(预测肿瘤细胞密度 1% 等值面),基于 FET+SEG 和 SEG 的结果。(a) 相对于 RTOG CTV 的相对体积。(b) 效率,即首次检测到复发时被 CTV 覆盖的 TC 百分比(详见正文)。© 效率与相对体积的比值。总体而言,基于 FET+SEG 和 SEG 的个性化 CTV 能在维持与 RTOG CTV 相当效率的同时,减少或保持相似的辐射体积。

Table J.16Paired t-test p-values for the comparison of the estimated parameters and metrics for synthetic (S1–S8) and patient data(P1–P8 and Q1–Q16) using different methods.
表 J.16使用不同方法对合成数据(S1–S8)和患者数据(P1–P8 和 Q1–Q16)的估计参数和指标进行比较的配对 t 检验 p-值。

Table L.17Percentage relative error of estimated parameters and the metrics, comparing effect of personalized pre-training (labeled S[1256])and fixed pre-training based on pre-trained model using characteristic parameter of S7 (labeled S[1256]∗ ). Personalized characteristicparameters give better results.
表 L.17估计参数和指标的相对误差百分比,比较个性化预训练(标记为 S12561256)与基于 S7 特征参数的固定预训练(标记为 S12561256∗)的效果。个性化特征参数的结果更优。