Title
题目
SUGAR: Spherical ultrafast graph attention framework for cortical surface registration
SUGAR:用于皮层表面配准的球形超快图注意力框架
01
文献速递介绍
基于表面的分析在解剖和功能神经影像学研究中变得越来越受欢迎(Coalson 等, 2018;Fischl, 2012;Van Essen, 2005)。表面网格提供了对大脑皮层复杂形态特征的合适表征(Dale 等, 1999;Van Essen 等, 2001, 1998)。与体积分析方法相比,这类分析通过皮层表面配准能够更准确地对齐不同个体的大脑皮层功能和解剖特征(Anticevic 等, 2008;Coalson 等, 2018;Ghosh 等, 2010;Jo 等, 2008;Oosterhof 等, 2011;Tucholka 等, 2012)。通常,皮层表面配准包括两个步骤:刚性配准和非刚性配准。刚性配准通过全局线性变换实现粗略的形态对齐,通常需要几分钟的处理时间。随后,非刚性配准进行逐顶点的局部变形,以实现精细和更精确的对齐。然而,非刚性配准的高计算复杂度导致处理时间长达数十分钟,例如 FreeSurfer 需要超过 20 分钟(Fischl 等, 1999a, 1999b)。这种计算效率低下给后续分析带来了挑战,例如解剖分区和群体平均分析,尤其是在处理大规模数据集时(Fischl 等, 2004;Yeo 等, 2011)。此外,非刚性变形仅以提高配准精度为目标,可能会导致拓扑错误和不合理的局部变形(Robinson 等, 2014;Yeo 等, 2009)。因此,在提高配准精度、保持拓扑结构和最小化配准形变之间取得平衡至关重要,尽管充满挑战。因此,配准的评估可以基于四个关键方面总结:计算效率、配准精度、拓扑保持和配准形变。过去二十年中,FreeSurfer 一直是刚性和非刚性皮层表面配准方法的先锋(Fischl 等, 1999a, 1999b)。然而,正如前文所述,FreeSurfer 在非刚性配准中的计算效率有限。Spherical Demons(SD)在提高非刚性配准效率方面取得了重大进展,在保持拓扑结构和确保高精度与形变控制的同时,在不到 5 分钟内完成了配准过程(Yeo 等, 2009)。多模态表面匹配(MSM)通过利用多模态特征(不仅仅是几何特征)实现了表面配准,其中一个变体展示了最先进的形变控制(Robinson 等, 2018, 2014)。然而,MSM 也带来了高计算负担。
Aastract
摘要
Cortical surface registration plays a crucial role in aligning cortical functional and anatomical features across individuals. However, conventional registration algorithms are computationally inefficient. Recently, learningbased registration algorithms have emerged as a promising solution, significantly improving processing efficiency. Nonetheless, there remains a gap in the development of a learning-based method that exceeds the stateof-the-art conventional methods simultaneously in computational efficiency, registration accuracy, and distortion control, despite the theoretically greater representational capabilities of deep learning approaches. To address the challenge, we present SUGAR, a unified unsupervised deep-learning framework for both rigid and non-rigid registration. SUGAR incorporates a U-Net-based spherical graph attention network and leverages the Euler angle representation for deformation. In addition to the similarity loss, we introduce fold and multiple distortion losses to preserve topology and minimize various types of distortions. Furthermore, we propose a data augmentation strategy specifically tailored for spherical surface registration to enhance the registration performance. Through extensive evaluation involving over 10,000 scans from 7 diverse datasets, we showed that our framework exhibits comparable or superior registration performance in accuracy, distortion, and test-retest reliability compared to conventional and learning-based methods. Additionally, SUGAR achieves remarkable sub-second processing times, offering a notable speed-up of approximately 12,000 times in registering 9,000 subjects from the UK Biobank dataset in just 32 min. This combination of high registration performance and accelerated processing time may greatly benefit large-scale neuroimaging studies
皮层表面配准在对齐不同个体的皮层功能和解剖特征方面起着至关重要的作用。然而,传统的配准算法计算效率低下。最近,基于学习的配准算法作为一种有前景的解决方案出现,显著提高了处理效率。然而,尽管深度学习方法在理论上具有更强的表征能力,但在计算效率、配准精度和形变控制方面同时超越当前最先进的传统方法的学习方法仍然存在空白。为了解决这一挑战,我们提出了SUGAR,这是一种用于刚性和非刚性配准的统一无监督深度学习框架。SUGAR结合了基于U-Net的球形图注意力网络,并利用欧拉角表示形变。除了相似性损失外,我们还引入了折叠损失和多种形变损失,以保持拓扑结构并最小化各种类型的形变。此外,我们提出了一种专门为球形表面配准设计的数据增强策略,以提高配准性能。通过对7个不同数据集的超过10,000次扫描进行广泛评估,我们展示了该框架在精度、形变和测试-重测可靠性方面的配准性能与传统方法和基于学习的方法相比具有可比性或更优的表现。此外,SUGAR实现了显著的亚秒级处理时间,在仅32分钟内完成了UK Biobank数据集中9,000名受试者的配准,速度提升约12,000倍。这种高配准性能与快速处理时间的结合,可能极大地促进大规模神经影像学研究。
Method
方法
In cortical surface registration, mapping cortical surfaces into spherical meshes is a commonly used method, which naturally preserves the topology. The process of surface registration involves deforming a moving sphere (M) to align with a fixed sphere (F), while simultaneously maximizing similarities, preserving topology, and minimizing distortions. Both M and F consist of N vertices {vi}N i=1, where vi* ∈ R3 is represented in the Cartesian coordinate (i.e. xyz-coordinate).
在皮层表面配准中,将皮层表面映射为球形网格是一种常用的方法,这种方法自然地保留了拓扑结构。表面配准的过程涉及将移动球体 (M) 变形以与固定球体 (F) 对齐,同时最大化相似性、保持拓扑结构并最小化形变。M 和 F 都由 N 个顶点 {v*i}N i=1 组成,其中 vi ∈ R³,表示为笛卡尔坐标(即 xyz 坐标)。
Conclusion
结论
In this study, we have presented the SUGAR framework, a comprehensive solution for both rigid and non-rigid cortical surface registration. The framework demonstrates exceptional performance in preserving the topology of deformations while achieving state-of-the-art results in terms of computational efficiency, registration accuracy, distortion control, and test-retest reliability. The accelerated framework with outstanding registration performance holds significant potential for facilitating large-scale neuroimaging studies. Furthermore, the SGAT architecture, combined with the incorporation of fold and distortion losses, as well as the introduced data augmentation strategy, offer ageneralizable approach that can be applied to various tasks involving spherical mesh representations.
在本研究中,我们提出了SUGAR框架,这是一个全面解决刚性和非刚性皮层表面配准的问题的方案。该框架在保持形变拓扑结构的同时,在计算效率、配准精度、形变控制和测试-重测可靠性方面取得了最先进的成果。这个加速框架凭借其卓越的配准性能,具有极大的潜力来推动大规模神经影像学研究。此外,S-GAT架构结合了折叠损失和形变损失的引入,以及提出的数据增强策略,提供了一种可推广的方法,能够应用于涉及球形网格表示的各种任务。
Figure
图

Fig. 1. Illustration of the SUGAR framework. The model inputs include the geometric features and Cartesian coordinates of the Moving (M) and Fixed (F) icospheres. The Cartesian coordinates are transformed (f) into spherical coordinates and further encoded (η) as higher-dimensional positional features. These geometric features and positional features are then fed into the spherical graph attention network (S-GAT). The S-GAT outputs a set of global Euler angle φ, which are transformed into a rotation tensor Φ = R(φ) in the spatial transform layer to rigidly align the input pairs, indicated by the orange flow. Subsequently, the rigidly registered Moved (M∘Φ)sphere replaces the original M as the input for the subsequent non-rigid registration, indicated by the blue flow. In the rigid registration, only a similarity term was used in the loss function. In the non-rigid registration, three types of distortion losses and a fold loss are applied in addition to the similarity term to constrain various distortions and eliminate folds.
图 1. SUGAR 框架示意图。模型输入包括移动球 (M) 和固定球 (F) 的几何特征和笛卡尔坐标。笛卡尔坐标通过变换函数 (f) 转换为球坐标,并进一步编码 (η) 为高维位置特征。这些几何特征和位置特征随后被输入到球形图注意力网络 (S-GAT) 中。S-GAT 输出一组全局欧拉角 φ,并在空间变换层中通过旋转张量 Φ = R(φ) 转换,以刚性对齐输入对,示意为橙色流动。接着,刚性配准后的移动球 (M∘Φ) 替换原始的 M,作为后续非刚性配准的输入,示意为蓝色流动。在刚性配准中,损失函数中仅使用了相似性项。而在非刚性配准中,除了相似性项之外,还应用了三种类型的形变损失和一个折叠损失,以约束各种形变并消除折叠现象。

Fig. 2. S-GAT architecture. The S-GAT is structured as a U-Net architecture. The GAT layer (yellow arrows) within the S-GAT learns the weights of the input features by attending to every node and edge in the icosphere. The current icosphere is then downsampled to the lower-resolution icosphere through the pooling layer (orange arrows). Once the S-GAT captures the most salient features, the icosphere begins to be upsampled to the higher-resolution icosphere through the unpooling layer (green arrows). These upsampled features are concatenated with the features from the corresponding pooling layer using a skip-connection strategy (gray arrows), iteratively restoring the original resolution of the icosphere. Finally, the S-GAT outputs a set of Euler angles. Each dot with different colors represents each node with different features, and each line with different thickness represents each edge with different weights. N* denotes the number of vertices in the icosphere icoi and Cj denotes the number of channels. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).
图 2. S-GAT 架构。S-GAT 采用 U-Net 架构。S-GAT 中的 GAT 层(黄色箭头)通过关注 icosphere 中的每个节点和边缘来学习输入特征的权重。当前的 icosphere 然后通过池化层(橙色箭头)下采样至低分辨率的 icosphere。当 S-GAT 捕获到最显著的特征后,icosphere 开始通过反池化层(绿色箭头)上采样至高分辨率的 icosphere。这些上采样的特征通过跳跃连接策略(灰色箭头)与对应池化层的特征进行拼接,迭代地恢复 icosphere 的原始分辨率。最终,S-GAT 输出一组欧拉角。图中每个不同颜色的点代表具有不同特征的节点,每条不同粗细的线代表具有不同权重的边缘。Ni 表示 icosphere icoi 中的顶点数,Cj 表示通道数。(关于此图例中颜色引用的解释,读者可参考文章的网络版本)。

Fig. 3. Comparison of parcellation accuracy across different methods. The Dice scores of anatomical parcellation between the manual annotations and automatically generated parcellation derived from different registration methods. For better illustration, we used the FreeSurfer as the benchmark method. Warm colors indicate parcels with higher Dice scores compared to FreeSurfer, and cool colors indicate parcels with lower Dice score compared to FreeSurfer. The dark red lines highlight areas with significantly higher and lower Dice scores than FreeSurfer, respectively. Our model yields 91.18 % of parcels with higher Dice scores and no areas significantly lower than FreeSurfer, outperforming other methods.
图 3. 不同方法间分区精度的比较。该图展示了手动标注与通过不同配准方法自动生成的解剖分区之间的 Dice 分数。为了更好地说明,我们使用 FreeSurfer 作为基准方法。暖色表示比 FreeSurfer 更高的 Dice 分数的区域,而冷色表示比 FreeSurfer 较低的 Dice 分数的区域。深红色线条分别突出显示了比 FreeSurfer 显著更高和更低 Dice 分数的区域。我们的模型在 91.18% 的区域中显示了更高的 Dice 分数,没有区域显著低于 FreeSurfer,表现优于其他方法。

Fig. 4. The group-average and standard deviation maps of sulcal depth. The leftmost sulcal depth map is the atlas. The upper panel presents group-average maps of sulcal depth derived from different registration methods across subjects from both the (a) ADRC and (b) HCP datasets. The lower panel displays the corresponding standard deviation maps. Notably, SUGAR consistently demonstrates more consistent alignment in the group-average maps and exhibits smaller variances, indicating improved registration accuracy in sulcal depth
图 4. 脑沟深度的组平均图和标准差图。最左侧的脑沟深度图是标准图谱。上方面板展示了通过不同配准方法在 (a) ADRC 和 (b) HCP 数据集的受试者中得到的脑沟深度组平均图。下方面板显示了相应的标准差图。值得注意的是,SUGAR 在组平均图中显示了更一致的对齐效果,并且方差较小,表明其在脑沟深度配准精度方面有所提升。

Fig. 5. Deformed spherical meshes with distortions from different methods. The deformed spherical meshes from different methods of a representative subject from the ADRC dataset are illustrated. Obvious distortion could be found in FreeSurfer, SD, MSM Pair, and S3Reg. MSM Strain and SUGAR achieved the smoothest deformation, with distortion that is hard to be discerned.
图 5. 不同方法的球形网格变形及形变情况。该图展示了来自 ADRC 数据集的一个代表性受试者的通过不同方法得到的球形网格变形。在 FreeSurfer、SD、MSM Pair 和 S3Reg 方法中可以看到明显的形变。而 MSM Strain 和 SUGAR 实现了最平滑的变形,几乎看不到形变。

Fig. 6. The average distortion maps across participants on the ADRC dataset. Group-average (a) areal, (b) shape, and © edge distortions from different methods are demonstrated. Darker colors indicate smaller distortions. SUGAR shows the least distortions in all types among all methods.
图 6. ADRC 数据集受试者的平均形变图。该图展示了不同方法的组平均 (a) 面积形变、(b) 形状形变和 © 边缘形变。颜色越深表示形变越小。SUGAR 在所有方法中显示了所有类型形变最小的情况。

Fig. 7. The average distortion maps across participants on the HCP dataset. MSM strain shows the least and the most evenly distributed areal distortions among all methods. SUGAR shows the least shape and edge distortions among all methods
图7. HCP 数据集受试者的平均形变图。MSM Strain 在所有方法中显示了最小且最均匀分布的面积形变。SUGAR 在所有方法中显示了最小的形状和边缘形变。

Fig. 8. Comparison of test-retest reliability in sulcal alignment. (a) The test-retest reliability in sulcal alignment is estimated in the MSC dataset, in which each of 10 subjects underwent four T1w scans. The brain maps show the group-average vertex-wise test-retest reliability from different methods. Darker colors indicate higher reliability. FreeSurfer shows the highest reliability, followed by SUGAR, both significantly higher than other methods. (b) The test-retest reliability is estimated in the CoRR-HNU dataset, in which each of 30 subjects underwent ten T1w scans. The reliability maps show consistent results with the MSC dataset.
图 8. 脑沟对齐的测试-重测可靠性比较。(a) 脑沟对齐的测试-重测可靠性在 MSC 数据集中进行估计,其中每位受试者进行了四次 T1w 扫描。脑图显示了不同方法的组平均顶点级测试-重测可靠性。颜色越深表示可靠性越高。FreeSurfer 显示了最高的可靠性,其次是 SUGAR,二者显著高于其他方法。(b) 测试-重测可靠性在 CoRR-HNU 数据集中进行估计,其中每位受试者进行了十次 T1w 扫描。可靠性图与 MSC 数据集的结果一致。
Table
表
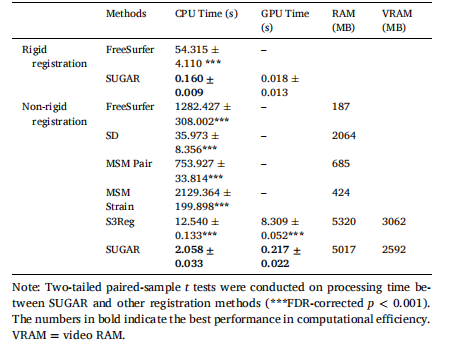
Table 1 Comparison of computational efficiency and memory costs between different registration methods.
表 1 不同配准方法之间的计算效率和内存消耗的比较。

Table 2 Comparison of rigid registration accuracy between FreeSurfer and SUGAR.
表 2 FreeSurfer 和 SUGAR 之间的刚性配准精度比较。

Table 3 Comparison of registration accuracy and spherical distortion between different registration methods (the ADRC dataset).
表3 不同配准方法之间的注册精度和球形畸变比较(ADRC数据集)。

Table 4 Comparison of registration accuracy and spherical distortion between different registration methods (the HCP dataset).
表 4 不同配准方法在配准精度和球形变形上的比较(HCP 数据集)。

Table 5 Comparison of computational efficiency, registration accuracy, and spherical distortion (the UKB dataset).
表 5 计算效率、配准精度和球形变形的比较(UKB 数据集)。

Table 6 Ablation study for positional encoding (PE).
表 6 位置编码(PE)消融实验。

Table 7 Ablation study for areal, angular, and distance losses
表 7 面积损失、角度损失和距离损失的消融实验。

Table 8 Ablation study for the data augmentation strategy (DA).
表 8 数据增强策略(DA)的消融实验。

Table 9 Ablation study for the data augmentation strategy (DA) in subject-to-subject registration.
表 9 在个体对个体配准中的数据增强策略(DA)消融实验。